Đề kiểm 15 phút - Đề số 3 - Bài 5 - Chương 3 - Hình học 9

Cho AB và AC là hai dây cung trong đường tròn (O). Gọi M là điểm chính giữa cảu cung AB, N là điểm chính giữa của cung AC. Các đường thẳng MN và AB cắt nhau tại E, MN và AC cắt nhau tại F. Chứng minh : \(AE = AF.\)

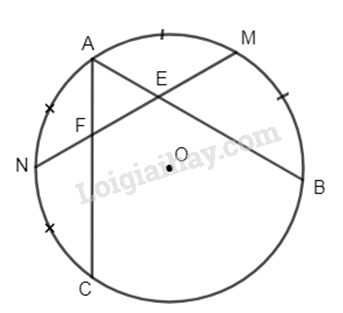
Trường hợp MN cắt AB và AC tại các điểm E, F ở bên trong đường tròn.

Ta có : \(\widehat {AEN} = \dfrac{{sd\overparen{AN} + sd\overparen{BM}} }{ 2}\)

\(\widehat {AFM} = \dfrac{{sd\overparen{AM} + sd\overparen{CN}} }{ 2}\)

Trong đó \(\overparen{ AN }= \overparen{CN}, \,\overparen{BM} = \overparen{AM}\) (gt)

\(\Rightarrow \widehat {AEM} = \widehat {AFM}\) hay \(∆AEF\) cân \(\Rightarrow AE = AF.\)

Trường hợp MN cắt AB, AC ở E và F nằm ngoài đường tròn hoặc một điểm ở bên trong, một điểm ở bên ngoài làm tương tự.