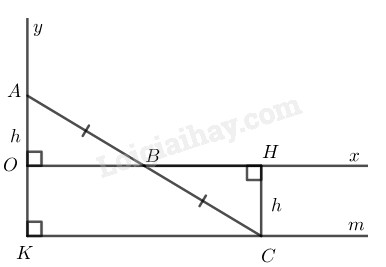
Vì điểm \(C\) đối xứng với điểm \(A\) qua điểm \(B\) \(⇒ BA = BC\)
Kẻ \(CH ⊥ Ox\)
Xét hai tam giác vuông \(AOB\) và \(CHB:\)
\(\widehat {AOB} = \widehat {CHB} = {90^0}\)
\(BA = BC\) (chứng minh trên)
\(\widehat {ABO} = \widehat {CBH}\) (đối đỉnh)
Do đó: \(∆ AOB = ∆ CHB\) (cạnh huyền, góc nhọn) \(⇒ CH = AO\)
\(A, O\) cố định \(⇒ OA\) không đổi nên \(CH\) không đổi.
\(C\) thay đổi cách \(Ox\) một khoảng bằng \(OA\) không đổi nên \(C\) chuyển động trên đường thẳng song song với \(Ox,\) cách \(Ox\) một khoảng \(OA.\)
Khi \(B\) trùng \(O\) thì \(C\) trùng với điểm \(K\) đối xứng với \(A\) qua điểm \(O.\)
Vậy \(C\) chuyển động trên tia \(Km // Ox,\) cách \(Ox\) một khoảng không đổi bằng \(OA.\)