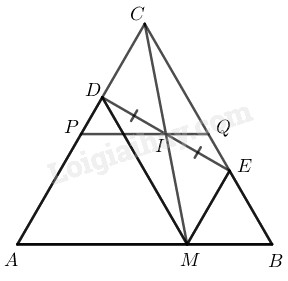
Gọi giao điểm của \(AD\) và \(BE\) là \(C.\)
\(∆ ABC\) có: \(\widehat A = {60^0}\) (vì \(∆ ADM\) đều)
\(\widehat B = {60^0}\) (vì \(∆ BEM\) đều)
Suy ra: \(∆ ABC\) đều, \(AC = AB = BC\) nên điểm \(C\) cố định
\(\widehat A = \widehat {EMB} = {60^0}\)
\(⇒ ME // AC\) (vì có cặp góc đồng vị bằng nhau)
hay \(ME // DC\)
\(\widehat {DMA} = \widehat B = {60^0}\)
\(⇒ MD // BC\) (vì có cặp góc đồng vị bằng nhau)
hay \(MD // EC\)
Tứ giác \(CDME\) là hình bình hành
\(I\) là trung điểm của \(DE\) nên \(I\) là trung điểm của \(CM\)
Kẻ \(CH ⊥ AB, IK ⊥ AB\) \(⇒ IK // CH\)
Trong \(∆ CHM\) ta có:
\(CI = IM\)
\(IK // CH\)
nên \(IK\) là đường trung bình của \(∆ CHM\) \(⇒ IK = \displaystyle {1 \over 2}CH\)
\(C\) cố định \(⇒ CH\) không đổi \(⇒ IK =\displaystyle{1 \over 2}CH\) không thay đổi nên \(I\) chuyển động trên đường thẳng song song \(AB,\) cách \(AB\) một khoảng bằng \(\displaystyle{1 \over 2}CH.\)
Khi \(M\) trùng với \(A\) thì \(I\) trùng trung điểm \(P\) của \(AC.\)
Khi \(M\) trùng với \(B\) thì \(I\) trùng với trung điểm \(Q\) của \(BC.\)
Vậy khi \(M\) chuyển động trên đoạn thẳng \(AB\) thì \(I\) chuyển động trên đoạn \(PQ\) (\(P\) là trung điểm của \(AC, Q\) là trung điểm của \(BC\))