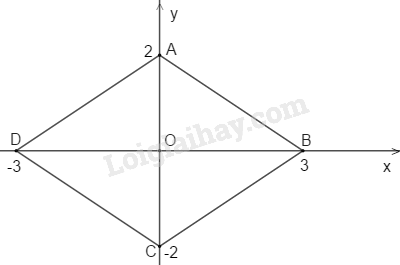
\(A(0; 2)\) và \(C(0; −2)\) nên hai điểm \(A\) và \(C\) đối xứng nhau qua \(O (0, 0)\) \(⇒ OA = OC\)
\(B(3; 0)\) và \(D(−3; 0)\) nên hai điểm \(B\) và \(D\) đối xứng qua \(O (0; 0)\) \(⇒ OB = OD\)
Tứ giác \(ABCD\) là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm mỗi đường)
\(Ox ⊥ Oy\) hay \(AC ⊥ BD\)
Vậy tứ giác \(ABCD\) là hình thoi
Trong \(∆ OAB\) vuông tại \(O.\) Theo định lý Pi-ta-go ta có:
\(\eqalign{ & A{B^2} = O{A^2} + O{B^2} \cr & A{B^2} = {2^2} + {3^2} = 4 + 9 = 13 \cr & AB = \sqrt {13} \cr} \)
Chu vi hình thoi bằng \(4\sqrt {13} \)