Chu vi hình thoi bằng \(16\, (m)\) nên độ dài một cạnh bằng:
\(16 : 4 = 4 \,(cm)\)
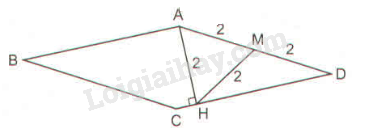
Gọi \(M\) là trung điểm của \(AD.\)
Trong tam giác vuông \(AHD\) ta có \(HM\) là trung tuyến thuộc cạnh huyền
\(HM = AM =\) \(\displaystyle {1 \over 2}\)\(AD=\) \(\displaystyle {1 \over 2}\)\(.4\) \(= 2\, (cm)\)
\(⇒ AM = HM = MD = 2\, cm\)
\(⇒ ∆ AHM\) đều
\( \Rightarrow \widehat {HAM} = {60^0}\) hay \(\widehat {HAD} = {60^0}\)
Trong tam giác vuông \(AHD\) ta có: \(\widehat {HAD} + \widehat D = {90^0}\)
\( \Rightarrow \widehat D = {90^0} - \widehat {HAD}\)\( = {90^0} - {60^0} = {30^0}\)
\( \Rightarrow \widehat B = \widehat D = {30^0}\) (tính chất hình thoi)
\(\widehat B + \widehat C = {180^0}\) (hai góc trong cùng phía bù nhau)
\( \Rightarrow \widehat C = {180^0} - \widehat B\)\( = {180^0} - {30^0} = {150^0}\)
\(\widehat A = \widehat C = {150^0}\) (tính chất hình thoi)