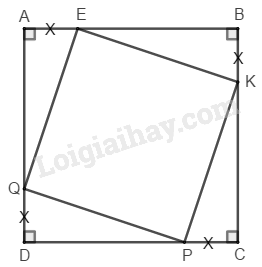
\(AB = BC = CD = DA\) (gt)
\(AE = BK = CP = DQ\) (gt)
Suy ra: \(EB = KC = PD = QA\)
- Xét \(∆ AEQ\) và \(∆ BKE :\)
\(AE = BK\) (gt)
\(\widehat A = \widehat B = {90^0}\)
\(QA = EB\) (chứng minh trên)
Do đó: \(∆ AEQ = ∆ BKE\, (c.g.c)\) \(⇒ EK = EQ\) (1)
- Xét \(∆ BKE\) và \(∆ CPK :\)
\(BK = CP\) (gt)
\(\widehat B = \widehat C = {90^0}\)
\(EB = KC\) (chứng minh trên)
Do đó: \(∆ BKE = ∆ CPK\, (c.g.c)\) \(⇒ EK = KP\) (2)
Xét \(∆ CPK\) và \(∆ DQP :\)
\(CP = DQ\) (gt)
\(\widehat C = \widehat D = {90^0}\)
\(DP = CK\) (chứng minh trên)
Do đó: \(∆ CPK = ∆ DQP\, (c.g.c)\) \(⇒ KP = PQ\) (3)
Từ (1), (2) và (3) suy ra: \(EK = KP = PQ = EQ\)
Tứ giác \(EKPQ\) là hình thoi.