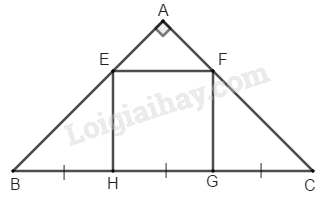
\(∆ ABC\) vuông cân tại \(A.\) \( \Rightarrow \widehat B = \widehat C = {45^0}\)
\(∆ BHE\) vuông tại \(H\) có \(\widehat B = {45^0}\)
\(⇒ ∆ BHE\) vuông cân tại \(H\) nên \(HB = HE\)
\(∆ CGF\) vuông cân tại \(G\) có \(\widehat C = {45^0}\)
\(⇒ ∆ CGF\) vuông cân tại \(G\) nên \(GC = GF\)
Ta có: \(BH = HG = GC\) (gt)
Suy ra: \(HE = HG = GF\)
\(EH // GF\) (hai đường thẳng cùng vuông góc với đường thẳng thứ ba)
nên tứ giác \(HEFG\) là hình bình hành (vì có một cặp cạnh đối song song bằng nhau)
có \(\widehat {EHG} = {90^0}\) do đó \(HEFG\) là hình chữ nhật
\(EH = HG\) (chứng minh trên)
Vậy \(HEFG\) là hình vuông.