

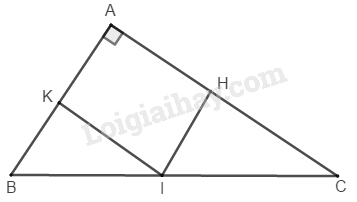
a. Ta có: \(IK // AC\) (gt)
hay \(IK // AH\)
\(IH // AB\) (gt)
hay \(IH // AK\)
Vậy tứ giác \(AHIK\) là hình bình hành (theo định nghĩa)
b. Hình bình hành \(AHIK\) là hình thoi nên đường chéo \(AI\) là phân giác.
Ngược lại \(AI\) là phân giác. Hình bình hành \(AHIK\) có đường chéo là phân giác của một góc nên hình bình hành \(AHIK\) là hình thoi.
Vậy nếu \(I\) là giao điểm của đường phân giác của với cạnh \(BC\) thì tứ giác \(AHIK\) là hình thoi.
c. Hình bình hành \(AHIK\) là hình chữ nhật
\( \Rightarrow \widehat A = {90^0}\) suy ra \(∆ ABC\) vuông tại \(A\)
Ngược lại \(∆ ABC\) có \(\widehat A = {90^0}\)
Suy ra: Hình bình hành \(AHIK\) là hình chữ nhật.
Vậy nếu \(∆ ABC\) vuông tại \(A\) thì tứ giác \(AHIK\) là hình chữ nhật.