Bài 2 trang 26 SGK Hình học 12
Lời giải
Bài Tập và lời giải
Đề bài
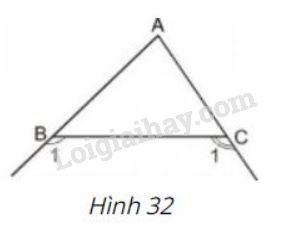
Cho tam giác \(ABC.\) Chứng minh rằng giao điểm của hai tia phân giác của hai góc ngoài \({B_1}\) và \({C_1}\) (h. 32) nằm trên tia phân giác của góc \(A.\)
Đề bài
Cho hai đường thẳng \(xx’, yy’\) cắt nhau tại \(O\) (h. 33).
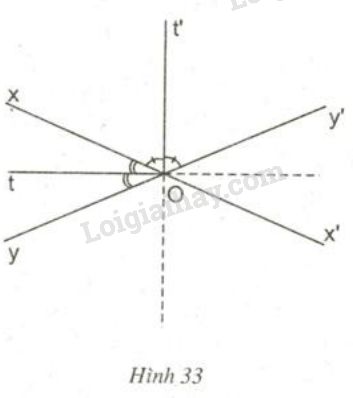
a) Chứng minh rằng hai tia phân giác \(Ot, Ot’\) của một cặp góc kề bù tạo thành một góc vuông.
b) Chứng minh rằng: Nếu \(M\) thuộc đường thẳng \( Ot\) hoặc thuộc đường thẳng \(Ot’\) thì \(M\) cách đều hai đường thẳng \(xx’\) và \( yy’.\)
c) Chứng minh rằng: Nếu \(M\) cách đều hai đường thẳng \(xx’, yy’\) thì \(M\) thuộc đường thẳng \(Ot\) hoặc thuộc đường thẳng \(Ot’\).
d) Khi \(M ≡ O\) thì khoảng cách từ \(M\) đến \(xx’\) và \(yy’\) bằng bao nhiêu ?
e) Em có nhận xét gì về tập hợp các điểm cách đều hai đường thẳng cắt nhau \(xx’, yy’.\)
Đề bài
Cho góc \(xOy\) khác góc bẹt. Trên tia \(Ox\) lấy hai điểm \(A\) và \(B\), trên tia \(Oy\) lấy hai điểm \(C\) và \(D\) sao cho \(OA = OC, OB = OD.\) Gọi \(I\) là giao điểm của hai đoạn thẳng \(AD\) và \(BC.\) Chứng minh rằng:
a) \(BC = AD\)
b) \(IA = IC, IB = ID\)
c) Tia \(OI\) là tia phân giác của góc \(xOy\).
Đề bài
Có mảnh sắt phẳng hình dạng một góc (h. 34) và một chiếc thước có chia khoảng. Làm thế nào để vẽ được tia phân giác của góc này?
Gợi ý: Áp dụng bài tập \(34.\)
Đề bài
Cho tam giác ABC vuông tại A có \(\widehat B = {60^0}\). Trên cạnh BC lấy điểm H sao cho \(HB = AB\). Đường thẳng vuông góc với BC tại H cắt AC tại D.
a) Chứng minh rằng: BD là tia phân giác của góc ABC.
b) Chứng tỏ \(\Delta B{\rm{D}}C\) cân.
Đề bài
Cho tam giác ABC có \(\widehat A = {120^0}\); các phân giác AD, BE, CF.
a) Chứng minh rằng DE là tia phân giác góc ngoài của \(\Delta AB{\rm{D}}{\rm{.}}\)
b) Chứng minh \(\widehat {E{\rm{D}}F} = {90^0}.\)
Đề bài
Cho tam giác ABC; các phân giác AD, BE, CF gặp nhau tại I.
a) Tính \(\widehat {IAC} + \widehat {IBC} + \widehat {IC{\rm{A}}}.\)
b) Kẻ IH vuông góc với BC (H thuộc BC). Chứng minh \(\widehat {BIH} = \widehat {CI{\rm{D}}}.\)
Đề bài
Cho tam giác ABC vuông tại A, biết AB = 3cm; AC = 4cm, phân giác của hai góc B và C cắt nhau tại I. Vẽ IH, IK lần lượt vuông góc với AB và AC. Tính khoảng cách từ I đến các cạnh của tam giác.