Bài 1 trang 26 SGK Hình học 12

Đề bài

 Dựa vào hình \(22\), hãy cho biết:

• \(AD\) có là đường trung tuyến của tam giác \(ABC\) hay không ?

• Các tỉ số \(\dfrac{{AG}}{{AD}}, \dfrac{{BG}}{{BE}},\dfrac{{CG}}{{CF}}\) bằng bao nhiêu?

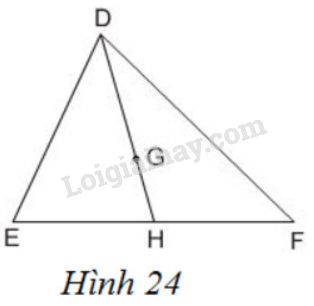
Đề bài

Cho \(G\) là trọng tâm của tam giác \(DEF\) với đường trung tuyến \(DH\). Trong các khẳng định sau đây, khẳng định nào đúng ?

\(\dfrac{DG}{DH}= \dfrac{1}{2}\); \(\dfrac{DG}{GH}= 3\) 

\(\dfrac{GH}{DH}= \dfrac{1}{3}\); \(\dfrac{GH}{DG}= \dfrac{2}{3}\)

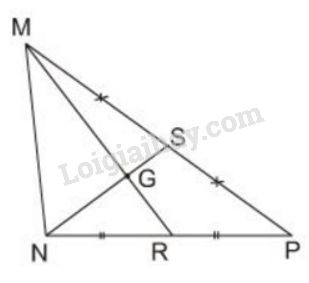
Đề bài

Cho hình \(25\). Hãy điền số thích hợp vào chỗ trống trong các đẳng thức sau:

a)  \(MG = … MR ;\) \(GR = … MR ;\) \(GR = … MG\)

b)  \(NS = ... NG;\) \(NS = …GS;\) \(NG = ... GS\)

Đề bài

Biết rằng: Trong một tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng một nửa cạnh huyền. Hãy giải bài toán sau:

Cho tam giác vuông \(ABC\) có hai cạnh góc vuông \(AB = 3\,cm, AC = 4\,cm.\) Tính khoảng cách từ đỉnh \(A\) tới trọng tâm \(G\) của tam giác \(ABC.\)

Đề bài

Chứng minh định lí: Trong một tam giác cân, hai đường trung tuyến ứng với hai cạnh bên thì bằng nhau.

Đề bài

Hãy chứng minh định lí đảo của định lí trên: Nếu tam giác có hai đường trung tuyến bằng nhau thì tam giác đó cân.

Đề bài

Cho tam giác \(DEF\) cân tại \(D\) với đường trung tuyến \(DI\).

a) Chứng minh \(∆DEI  = ∆DFI.\)

b) Các góc \(DIE\) và góc \(DIF\) là những góc gì?

c) Biết \(DE = DF = 13\,cm,\) \(EF = 10\,cm,\) hãy tính độ dài đường trung tuyến \(DI.\)

Đề bài

Cho \(G\) là trọng tâm của tam giác đều \(ABC.\) Chứng minh rằng:

                   \(GA = GB = GC.\)

Hướng dẫn: Áp dụng định lí ở bài tập \(26.\)

Đề bài

Gọi \(G\) là trọng tâm của tam giác \(ABC\). Trên tia \(AG\) lấy điểm \(G’\) sao cho \(G\) là trung điểm của \(AG’\).

a) So sánh các cạnh của tam giác \(BGG’\) với các đường trung tuyến của tam giác \(ABC.\)

b) So sánh các đường trung tuyến của tam giác \(BGG’\) với các cạnh của tam giác \(ABC.\)

Đề bài

Cho tam giác ABC, trung tuyến BM. Trên tia BM lấy điểm G sao cho . Trên \(GM =\dfrac {1 }{ 2}GB\) tia đối của tia MB lấy D sao cho G là trung điểm của BD. Gọi E là trung điểm của CD và I là giao điểm của GE với CM. Chứng minh rằng: I là trọng tâm của \(\Delta GC{\rm{D}}{\rm{.}}\) 

Đề bài

Cho tam giác ABC cân tại A, kẻ AH vuông góc với BC (H thuộc BC) trên tia AH lấy E sao cho H là trung điểm của AE. Trên tia đối của tia CB lấy F sao cho \(CF = BC\). Gọi M là trung điểm EB.

Chứng minh rằng: A, C, M thẳng hàng.

Đề bài

Cho tam giác ABC trên tia đối của tia AB lấy D sao cho \(AD = AB\). Lấy G thuộc AC sao cho \(AG = \dfrac{1 }{3}AC.\) Tia DG cắt BC ở E. Qua E vẽ đường thẳng song song với BD; qua D vẽ đường thẳng song song với BC, hai đường thẳng này cắt nhau ở F. Gọi M là giao điểm của EF và CD. 

Chứng minh rằng: B, G, M thẳng hàng.