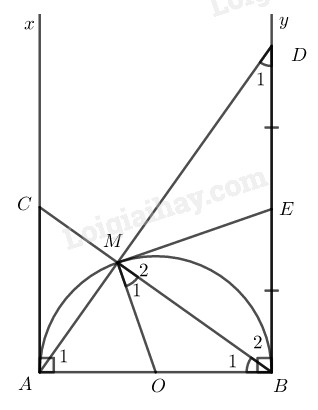
\(a)\) \(\widehat {{B_1}} = \widehat {{D_1}}\) ( cùng phụ với \(\widehat {{A_1}}\)).
Xét \(∆ABC\) và \(∆BDA\) có:
\(\widehat {{B_1}} = \widehat {{D_1}}\)
\(\widehat A = \widehat B = 90^\circ \)
\(∆ABC\) đồng dạng với \(∆BDA \;\;(g.g)\) suy ra:
\(\displaystyle{{AB} \over {BD}} = {{AC} \over {AB}}\), do đó \(AC . BD = AB^2\)
\(b)\) Áp dụng định lí trong tam giác vuông đường trung tuyến ứng với canh huyền thì bằng nửa cạnh huyền.
Ta có trong \(∆MBD\) có \(ED = EM = EB\)
\(∆EBM\) cân nên \(\widehat {{M_2}} = \widehat {{B_2}}\)\((1)\)
\(∆MOB\) cân tại \(O\) nên \(\widehat {{M_1}} = \widehat {{B_1}}\) \((2)\)
Từ \((1)\) và \((2)\) suy ra
\(\widehat {{M_1}} + \widehat {{M_2}}\) = \(\widehat {{B_1}} + \widehat {{B_2}}\) = \(90^\circ \),
tức là \(ME ⊥ OM\) tại \(M.\)
Vậy \(ME\) là tiếp tuyến của nửa đường tròn.