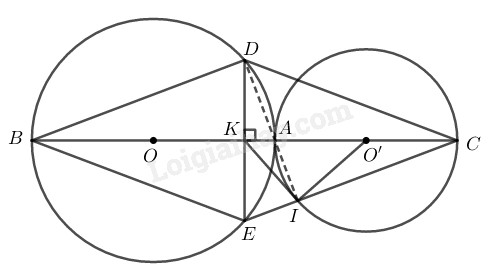
\(a)\) Vì đường tròn \((O)\) và \((O')\) tiếp xúc ngoài tại \(A\) nên \(O, A\) và \(O'\) thẳng hàng.
Ta có: \(KB = KC (gt)\)
Trong đường tròn \((O)\) ta có: \( AB ⊥ DE\) tại \(K\)
Suy ra: \(KD = KE\) ( đường kính vuông góc với dây cung)
Tứ giác \(BDCE\) có hai đường chéo cắt nhau tại trung điểm của mỗi đường nên nó là hình bình hành.
Lại có: \(BC ⊥ DE\)
Suy ra tứ giác \(BDCE\) là hình thoi.
\(b)\) Tam giác \(ABD\) nội tiếp trong đường tròn \((O)\) có \(AB\) là đường kính nên vuông tại \(D.\)
Suy ra: \(AD ⊥ BD\)
Tứ giác \(BDCE\) là hình thoi nên \(EC // BD\)
Suy ra: \(EC ⊥ AD\;\; (1)\)
Tam giác \(AIC\) nội tiếp trong đường tròn \((O')\) có \(AC\) là đường kính nên vuông tại \(I.\)
Suy ra: \(AI ⊥ CE\;\;(2)\)
Từ \((1)\) và \((2)\) suy ra \(AD\) trùng với \(AI\)
Vậy \(D, A, I\) thẳng hàng.
c) Tam giác \(DIE\) vuông tại \(I\) có \(IK\) là trung tuyến thuộc cạnh huyền \(DE\) nên:
\(KI = KD = \displaystyle {1 \over 2}ED\) ( tính chất tam giác vuông)
Suy ra tam giác \(IKD\) cân tại \(K\)
Suy ra: \(\widehat {KID} = \widehat {KDI}\) hay \(\widehat {KIA} = \widehat {KDA}\) \((3)\)
Ta có: \(O'A = O'I ( = R)\) nên tam giác \(O'IA\) cân tại \(O'\)
Suy ra: \(\widehat {O'AI} = \widehat {O'IA}\) ( tính chất tam giác cân)
Mà: \(\widehat {O'AI} = \widehat {KAD}\) (đối đỉnh)
Suy ra: \(\widehat {O'IA} = \widehat {KAD}\) \( (4)\)
Từ \((3)\) và \((4)\) suy ra: \(\widehat {KIO'} = 90^\circ \) hay \(KI ⊥ O'I\) tại \(I.\)
Vậy \(KI\) là tiếp tuyến của đường tròn \((O').\)