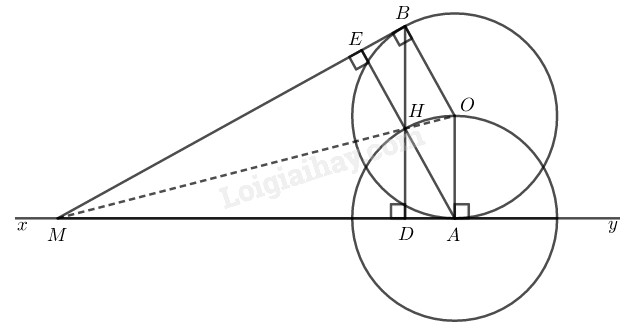
\(a)\) Xét \(∆MBO\) và \(∆MAO\) có:
\(MO\) chung
\(OA=OB\)
Nên \(∆MBO = ∆MAO\) (cạnh huyền – cạnh góc vuông).
Suy ra \(\widehat {BMO} = \widehat {OMA}\) \((1)\)
Gọi \(BD, AE \) là các đường cao của \(∆MAB\).
Xét \(∆MAE\) và \(∆MBD\) có :
\(MA=MB\)
\(\widehat {EMA} = \widehat {DMB}\)
Nên \(∆MAE = ∆MBD\) (cạnh huyền – góc nhọn).
Suy ra \(ME = MD\).
Xét \(∆MHE\) và \(∆MHD\) có:
\(ME = MD\)
\(MH\) chung
\(∆MHE = ∆MHD\) (cạnh huyền – cạnh góc vuông).
Nên \(\widehat {EMH} = \widehat {DMH}\) \((2).\)
Từ \((1)\) và \((2)\) suy ra\(MH\) và \(MO\) đều là tia phân giác của góc \(\widehat {AMB}\) nên \(M, H, O\) thẳng hàng.
\(b)\) Tứ giác \(AOBH\) có
\(BH // OA\) (cùng vuông góc với \(MA\)),
\(AH // OB\) (cùng vuông góc với \(MB\)).
Suy ra tứ giác \(AOBH\) là hình bình hành, mà \(OA = OB\) nên từ giác \(AOBH\) là hình thoi.
\(c)\) Ta có \(HA=OA\) (do \(AOBH\) là hình thoi),
Nên \(H\) cách \(A\) cố định một khoảng bằng \(OA\) không đổi khi \(M\) chuyển động trên \(xy\) thì di chuyển trên đường tròn \((A ; AO).\)