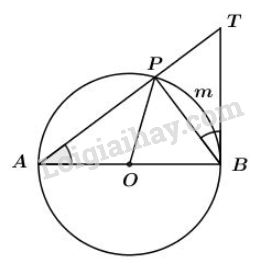
Ta có: \(\widehat{PBT}\) là góc tạo bởi tiếp tuyến \(BT\) và dây cung \(BP\) chắn cung \(\overparen{PmB}\).
\(\Rightarrow \widehat{PBT} = \dfrac{1}{2} sđ \overparen{PmB}\) (1)
Lại có: \(\widehat{PAO}\) là góc nội tiếp chắn cung \(\overparen{PmB}\)
\(\Rightarrow \widehat{PAO} = \dfrac{1}{2} sđ \overparen{PmB}\) (2)
Mặt khác: \(\widehat{PAO}= \widehat{APO}\) (\(∆OAP \, \, cân\, \, tại \, \, O)\) (3)
Từ (1), (2), (3), suy ra \(\widehat{APO} =\widehat{PBT}\) (đpcm)