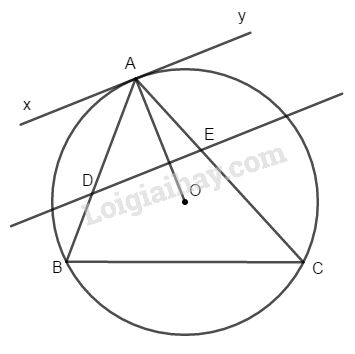
Ta có : DE // xAy
\(\Rightarrow \widehat {xAD} = \widehat {ADE}\) ( so le trong)
Lại có \(\widehat {xAD} = \widehat {BCA}\) ( góc giữa tiếp tuyến và một dây bằng góc nội tiếp cùng chắn cung AB) => \(\widehat {ADE} = \widehat {BCA}\).
Xét \(∆ABC\) và \(∆ADE\) có:
+) \(\widehat {BAC}\) chung
+) \(\widehat {ADE} = \widehat {BCA}\)
Do đó \(∆ABC\) đồng dạng \(∆AED\) (g.g)
\(\Rightarrow \dfrac{{AB}}{ {AC}} = \dfrac{{AE} }{ {AD}}\)
\(\Rightarrow AB.AD = AC.AE.\)