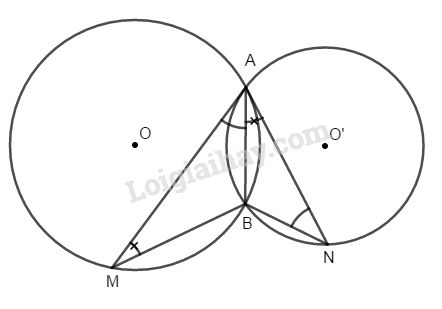
Hai tam giác ABM và NBA có :
+) \(\widehat {AMB} = \widehat {BAN}\)
+) \(\widehat {ANB} = \widehat {MAB}\) ( góc giữa tiếp tuyến và một dây bằng góc nội tiếp cùng chắn cung AB)
\(∆ABM\) đồng dạng \(∆NBA\) (g.g)
\(\Rightarrow\dfrac{{AB}}{{NB}} = \dfrac{{MB} }{ {AB}}\)
\(\Rightarrow AB^2= MB.NB\) và có \(\widehat {MBA} = \widehat {NBA}\).