\(\eqalign{
& a)\,\,{\left( {a + b} \right)^2} - {\left( {a - b} \right)^2} \cr
& = ({a^2} + 2ab + {b^2}) - ({a^2} - 2ab + {b^2}) \cr
& = {a^2} + 2ab + {b^2} - {a^2} + 2ab - {b^2} \cr
& = \left( {{a^2} - {a^2}} \right) + 2ab + 2ab + \left( {{b^2} - {b^2}} \right) \cr
& = 4ab \cr} \)
Cách 2:
\(\eqalign{
& {\left( {a + b} \right)^2} - {\left( {a - b} \right)^2} \cr
& = \left[ {\left( {a + b} \right) + \left( {a - b} \right)} \right].\left[ {\left( {a + b} \right) - \left( {a - b} \right)} \right] \cr
& = \left( {a + b + a - b} \right)\left( {a + b - {\rm{ }}a + b} \right) \cr
& = 2a.2b = 4ab \cr} \)
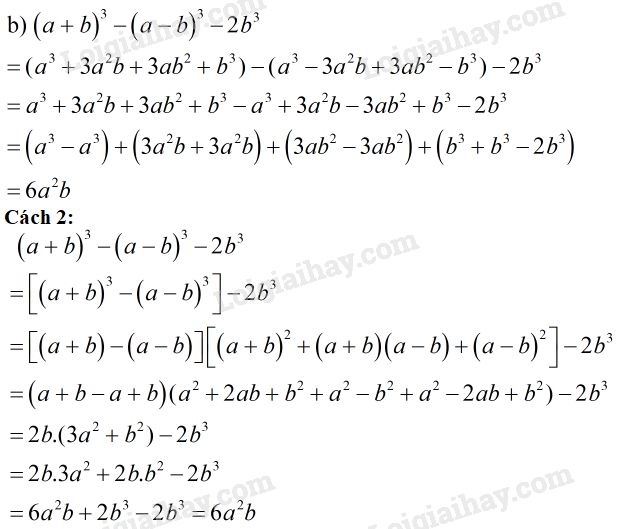
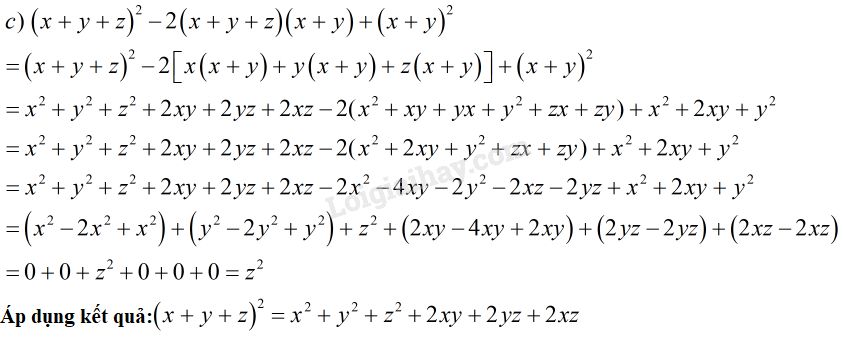
Cách 2:
Đặt \(A=x+y+z; B=x+y\)
Ta có:
\(\eqalign{
& {\left( {x + y + z} \right)^2} - 2\left( {x + y + z} \right)\left( {x + y} \right) + {\left( {x + y} \right)^2} \cr
& = {A^2} - 2AB + {B^2} = {\left( {A - B} \right)^2} \cr
& = {\left[ {\left( {x + y + z} \right) - \left( {x + y} \right)} \right]^2} \cr
& = {\left( {x + y + z - x - y} \right)^2} = {z^2} \cr} \)