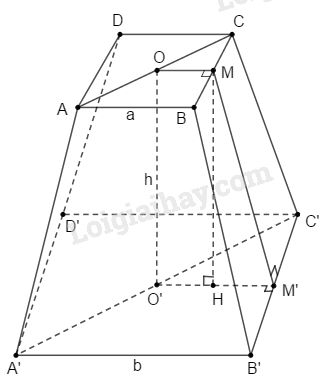
Xét hình chóp cụt đều \(ABCD.A’B’C’D’\) như hình vẽ.
Gọi \(M, M’\) thứ tự là trung điểm của \(BC, B’C’.\) Khi đó \(MM’\) là đường cao của hình thang cân \(BCC’B’\).
Do đó diện tích xung quanh của hình chóp cụt đều là:
\(\displaystyle{S_{xq}} = 4.{{a + b} \over 2}.MM' \)\(\,= \left( {2a + 2b} \right).MM'\)
Theo giả thiết, diện tích xung quanh bằng tổng diện tích hai đáy ta có:
\(\left( {2a + 2b} \right).MM' = {a^2} + {b^2}\)
hay \( \displaystyle MM' = {{{a^2} + {b^2}} \over {2\left( {a + b} \right)}}\) (1)
Dễ thấy \(OM // O’M’\) nên \(OM\) và \(O’M’\) xác định mặt phẳng \((OMM’O’)\).
Trong mặt phẳng \((OMM’O’)\), kẻ \(MH ⊥ O’M’\). Khi đó: \(HM’ = O’M’ - O’H = \displaystyle {{b - a} \over 2}\)
Áp dụng định lí Pytago vào tam giác vuông \(MHM’ \), ta có:
\(MM{'^2} = M{H^2} + HM{'^2} \)\(\,\displaystyle = {h^2} + {\left( {{{b - a} \over 2}} \right)^2}\) (2)
Từ (1) và (2) suy ra:
\(\begin{array}{l}{h^2} + {\left( {\dfrac{{b - a}}{2}} \right)^2} = \dfrac{{{{\left( {{a^2} + {b^2}} \right)}^2}}}{{4{{\left( {a + b} \right)}^2}}}\\ \Rightarrow {h^2} = \dfrac{{{{\left( {{a^2} + {b^2}} \right)}^2}}}{{4{{\left( {a + b} \right)}^2}}} - \dfrac{{{{\left( {b - a} \right)}^2}}}{4}\\ = \dfrac{{{{\left( {{a^2} + {b^2}} \right)}^2} - {{\left( {b - a} \right)}^2}.{{\left( {a + b} \right)}^2}}}{{4{{\left( {a + b} \right)}^2}}}\\ = \dfrac{{{{\left( {{a^2} + {b^2}} \right)}^2} - {{\left[ {\left( {b - a} \right).\left( {a + b} \right)} \right]}^2}}}{{4{{\left( {a + b} \right)}^2}}}\\ = \dfrac{{{{\left( {{a^2} + {b^2}} \right)}^2} - {{\left( {{b^2} - {a^2}} \right)}^2}}}{{4{{\left( {a + b} \right)}^2}}}\\ = \dfrac{{{a^2}{b^2}}}{{{{\left( {a + b} \right)}^2}}}\end{array}\)
Vậy \(\displaystyle h = {{ab} \over {a + b}}\).