Bài 5 trang 92 SGK Hình học 12

Đề bài

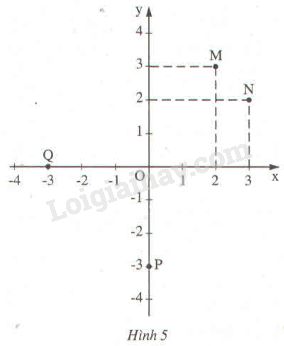
a) Viết tọa độ các điểm \(M, N, P, Q\) trong hình \(5.\)

b) Em có nhận xét gì về tọa độ của các cặp điểm \(M\) và \(N, P\) và \(Q.\)

Đề bài

Vẽ một hệ trục tọa độ và đánh dấu vị trí các điểm:

\(\displaystyle A(2; - 1,5),B\left( { - 3;{3 \over 2}} \right),C(2,5;0)\).

Đề bài

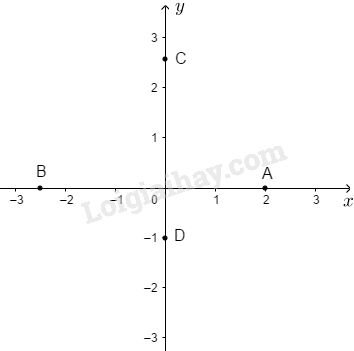
Xem hình 6, hãy cho biết:

a) Tung độ của các điểm \(A, B.\)

b) Hoành độ của các điểm \(C, D.\)

c) Tung độ của một điểm bất kì trên trục hoành và hoành độ của một điểm bất kỳ trên trục tung.

Đề bài

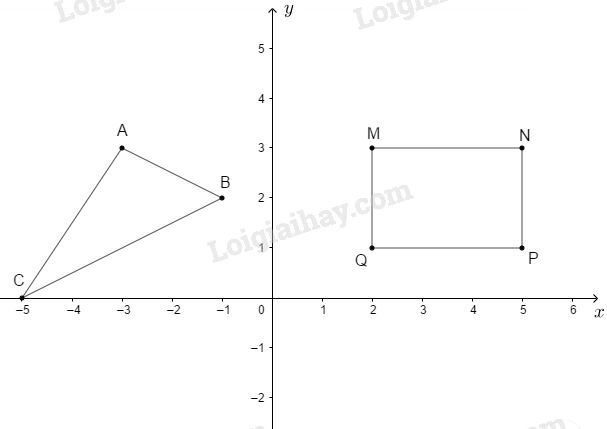
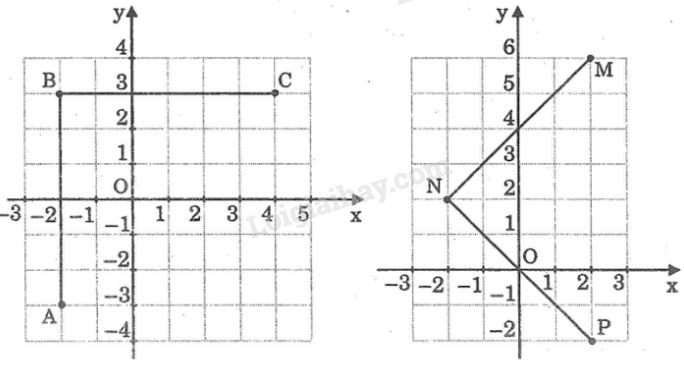
Tìm tọa độ các đỉnh của hình chữ nhật \(MNPQ \) và của tam giác \(ABC\) trong hình 7.

Đề bài

Vẽ một hệ trục \(Oxy\) và đánh dấu các điểm:

\(G(-2; -0,5), H(-1; -0,5),\)\(\, I(-1; -1,5), K(-2; -1,5)\).

Tứ giác \(GHIK\) là hình gì?

Đề bài

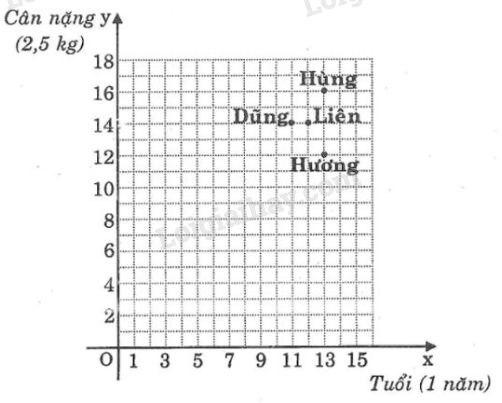
Cân nặng và tuổi của bốn bạn được biểu diễn trên mặt phẳng tọa độ (hình 8) (Mỗi đơn vị trên trục hoành biểu thị 1 năm, mỗi đơn vị trên trục tung biểu thị 2,5kg). Hỏi:

a) Ai là người nặng nhất và nặng bao nhiêu?

b) Ai là người ít tuổi nhất và bao nhiêu tuổi?

c) Giữa Liên và Hương, ai nặng hơn và ai nhiều tuổi hơn?

Đề bài

Vẽ một hệ trục tọa độ và đường phân giác của các góc phần tư thứ I, III.

a) Đánh dấu điểm \(A\) nằm trên đường phân giác đó và có hoành độ là \(2.\) Điểm \(A\) có tung độ là bao nhiêu?

b) Em có dự đoán gì về mối quan hệ giữa tung độ và hoành độ của một điểm \(M\) nằm trên đường phân giác đó?

Đề bài

Tìm tọa độ của đỉnh thứ tư của hình vuông trong mỗi trường hợp dưới đây (hình 9).

Bài 6.1

Điền vào chỗ trống các từ thích hợp.

a) Mỗi điểm \(M\) xác định……\((x_0; y_0)\). Ngược lại, mỗi cặp số \((x_0; y_0)\)……điểm \(M\).

b) Cặp số \((x_0; y_0)\) là tọa độ của điểm \(M\), \(x_0\) là……………và \(y_0\) là…………của điểm \(M\).

c) Điểm \(M\) có tọa độ……………… được kí hiệu là \(M(x_0; y_0).\)