Bài 1. Căn bậc hai
Bài Tập và lời giải
Tìm các căn bậc hai của mỗi số sau:
a) 9; b) \(\dfrac{4}{9}\); c) 0,25; d) 2.
Tìm căn bậc hai số học của mỗi số sau:
a) 49; b) 64; c) 81; d) 1,21.
Tìm các căn bậc hai của mỗi số sau
a) \(64\) b) \(81\) c) \(1,21\)
So sánh
a) 4 và \(\sqrt {15} \) ; b) \(\sqrt {11} \) và 3.
Tìm số \(x\) không âm, biết:
a) \(\sqrt x>1\) b) \(\sqrt x<3\)
b) \(\sqrt x
Tìm căn bậc hai số học của mỗi số sau rồi suy ra căn bậc hai của chúng
121; 144; 169; 225; 256; 324; 361; 400.
So sánh
a) \(2\) và \(\sqrt{3}\) ; b) \(6\) và \(\sqrt{41}\) ; c) \(7\) và \(\sqrt{47}\).
Dùng máy tính bỏ túi, tính giá trị gần đúng của nghiệm mỗi phương trình sau (làm tròn đến chữ số thập phân thứ \(3\)):
a) \(x^2 = 2\); b) \(x^2 = 3\);
c) \(x^2 = 3,5\); d) \(x = 4,12\);
Tìm số x không âm, biết:
a) \(\sqrt{x}=15\); b) \(2\sqrt{x}=14\);
c) \(\sqrt{x}<\sqrt{2}\); d) \(\sqrt{2x}<4\).
Đố. Tính cạnh một hình vuông, biết diện tích của nó bằng diện tích của một hình chữ nhật có chiều rộng 3,5m và chiều dài 14m.
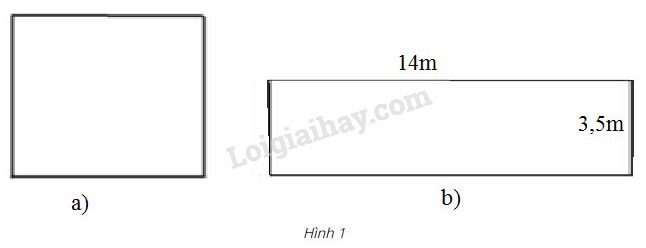
\( x^2 =49 \Leftrightarrow x=\pm \sqrt {49} \Leftrightarrow x = \pm 7\).
Vì \(x > 0\) nên \(x = 7\).
Vậy độ dài cạnh hình vuông là \(7m\).
Bài 1. (7 điểm) Hãy khoanh tròn vào chữ cái trước câu trả lời đúng
Câu 1. Biểu thức \(\sqrt {1 - 2x} \) xác định khi
A.\(x \ge \dfrac{1}{2}\) B. \(x \le \dfrac{1}{2}\)
C. \(x > \dfrac{1}{2}\) D. \(x < \dfrac{1}{2}\)
Câu 2. Điều kiện xác định của biểu thức \(\dfrac{{\sqrt x + 1}}{{x - \sqrt x }}\) là
A.\(x \ne 0\) B. \(x > 0,x \ne 1\)
C. \(x \ge 0\) D. \(x \ge 0,x \ne 1\)
Câu 3. Biểu thức \(\sqrt {\dfrac{1}{{x - 1}}} + \sqrt {2 - x} \) có nghĩa khi
A.\(x > 2\) B. \(x < 1\)
C. \(1 < x \le 2\) D. \(x \le 2,x \ne 1\)
Câu 4. Căn bậc hai số học của 64 là
A. 8 và -8 B. -8
C. 8 D. 32.
Câu 5. Kết quả phép tính\(\sqrt {{{(\sqrt 3 - \sqrt 2 )}^2}} \) là
A.\(\sqrt 3 - \sqrt 2 \) B. \(\sqrt 2 - \sqrt 3 \)
C. \( \pm (\sqrt 3 - \sqrt 2 )\) D. 1
Câu 6. Kết quả của phép tính \((2\sqrt 3 + \sqrt 2 )(2\sqrt 3 - \sqrt 2 )\) là
A.\(4\sqrt 3 \) B. \(2\sqrt 2 \)
C. 10 D. 14
Câu 7. Giá trị của biểu thức \({1 \over {2 + \sqrt 3 }} - {1 \over {2 - \sqrt 3 }}\) bằng
A.4 B. 0
C. \( - 2\sqrt 3 \) D. \(2\sqrt 3 \)
Câu 8. Giá trị của biểu thức \(\sqrt 3 - \sqrt {48} + \sqrt {12} \) là
A.\( - \sqrt 3 \) B. \(\sqrt 3 \)
C. \( - 2\sqrt 3 \) D. \(2\sqrt 3 \)
Câu 9. Giá trị của biểu thức \(\sqrt {{{(1 - \sqrt 2 )}^2}} - \sqrt {{{(1 + \sqrt 2 )}^2}} \) là
A.0 B. -2
C.\( - \sqrt 2 \) D. \( - 2\sqrt 2 \)
Câu 10. Giá trị của biểu thức \(\)\(\left( {\sqrt {27} - 3\sqrt {\dfrac{4}{3}} + \sqrt {12} } \right):\sqrt 3 \) bằng
A.\(\sqrt 3 \) B. \(2\sqrt 3 \)
C. \( - 2\sqrt 3 \) D.3
Câu 11. Giá trị của biểu thức \(\)\(\dfrac{{\sqrt 5 }}{{\sqrt {80} }}.\dfrac{{\sqrt {90} }}{{\sqrt {10} }}\) bằng
A.16 B.0,75
C. 4 D. 0,25.
Câu 12. Kết quả rút gọn của biểu thức \(\dfrac{{\sqrt {{x^2} - 6x + 9} }}{{x - 3}}\) với \(x > 3\) là
A.-1 B. 1
C. \( \pm 1\) D. kết quả khác.
Câu 13. Kết quả rút gọn của biểu thức \({x^2}{y^2}.\sqrt {\dfrac{9}{{{x^2}{y^4}}}} \) với x
A. \(3xy\) B.\({x^2}y\)
C. \(-3x\) D. \(-3xy.\)
Câu 14. Tất cả các giá trị của x thỏa mãn \(\sqrt {4{x^2} + 4x + 1} = 7\) là
A. \(x=3\) B. \(x = \dfrac{{ - 7}}{2}\)
C. \(x=-3\) D. \(x=-4;x=3.\)
Bài 2. (3 điểm) Điền x vào cột đúng hoặc sai cho thích hợp
|
Khẳng định |
Đúng |
Sai |
|
Số 0 là căn bậc hai số học của 0 |
|
|
|
Giá trị nhỏ nhất của biểu thức \(\sqrt {{x^2} + 4x + 5} \) là 5 |
|
|
|
Với a>b>0 thì \(\sqrt a - \sqrt b < \sqrt {a - b} \) |
|
|
|
Với a>0 và b>0 thì \(\sqrt a + \sqrt b > \sqrt {a + b} \) |
|
|
|
Với mọi số a, ta có \(\sqrt {{a^2}} = a\) |
|
|
|
\(\sqrt {\dfrac{a}{b}} = \dfrac{{\sqrt a }}{{\sqrt b }}\) với mọi a và b |
|
|
Bài 1. So sánh (không dùng máy tính hay bảng số):
a. 2 và \(\sqrt 5 \)
b. 2 và \(\sqrt 5 - 3\)
Bài 2. Tìm x, biết:
a. \({x^2} = 2\)
b. \({x^2} = 5\)
Bài 3. Tìm x, biết:
a. \(\sqrt x < \sqrt 2 \)
b. \(\sqrt x > \sqrt {2 - x} \)
Bài 1. Chứng minh rằng nếu \(a > 1\) thì \(a > \sqrt a .\)
Bài 2. Chứng minh rằng với mọi x, ta có : \(\sqrt {{x^2} + 2x + 5} \ge 2.\)
Bài 3. So sánh : \(\sqrt 3 - 5\) và \(-2\) (không dùng máy tính bỏ túi hay bảng số).
Bài 1. Tìm x, biết :
a. \(\sqrt {x + 2} = \sqrt {4 - x} \)
b. \(\sqrt {6 - 4x + {x^2}} - x = 4\)
Bài 2. So sánh : \(\sqrt 2 + \sqrt 3 \) và 2 ( không dùng máy tính hay bảng số).
Bài 3. Chứng minh rằng với a và b không âm, ta có: \({{a + b} \over 2} \ge \sqrt {ab} \).
Bài 1. Tìm x, biết :
a. \(\sqrt {1 - x} > 2\)
b. \(\sqrt {4 - x} \le 2\)
Bài 2. Tìm x, biết: \(\sqrt {{x^2} + 1} - x = 3\)
Bài 3. Chứng minh rằng với mọi x, ta có: \(\sqrt {{x^2} + 4} \ge 2\)
