Bài 4. Liên hệ giữa phép chia và phép khai phương

Tính và so sánh: \(\displaystyle \sqrt {{{16} \over {25}}} \) và \(\displaystyle {{\sqrt {16} } \over {\sqrt {25} }}\)

Tính

a) \(\displaystyle \sqrt {{{226} \over {256}}} \)

b) \(\sqrt {0,0196} \)

Tính: a) \(\displaystyle {{\sqrt {999} } \over {\sqrt {111} }}\)                     b) \(\displaystyle {{\sqrt {52} } \over {\sqrt {117} }}\)

Rút gọn

a) \(\sqrt {\dfrac{{2{a^2}{b^4}}}{{50}}} \)         b) \(\dfrac{{\sqrt {2a{b^2}} }}{{\sqrt {162} }}\)  với \(a \ge 0.\)

Tính:

a) \( \sqrt{\dfrac{289}{225}}\);                                 b) \( \sqrt{2\dfrac{14}{25}}\);

c) \( \sqrt{\dfrac{0,25}{9}}\) ;                               d) \( \sqrt{\dfrac{8,1}{1,6}}\).

Tính

a) \( \dfrac{\sqrt{2}}{\sqrt{18}}\);                                   b) \( \dfrac{\sqrt{15}}{\sqrt{735}}\);

c) \( \dfrac{\sqrt{12500}}{\sqrt{500}}\);                                d) \( \dfrac{\sqrt{6^{5}}}{\sqrt{2^{3}.3^{5}}}\).

Rút gọn các biểu thức sau:

a) \( \dfrac{y}{x}.\sqrt{\dfrac{x^{2}}{y^{4}}}\) với \(x > 0,\ y ≠ 0\);              

b) 2\( y^{2}\).\( \sqrt{\dfrac{x^{4}}{4y^{2}}}\) với \(y < 0\);

c) \(5xy. \sqrt{\dfrac{25x^{2}}{y^{6}}}\) với \(x < 0,\ y > 0\);        

d) \( 0,2x^{3}y^{3}.\sqrt{\dfrac{16}{x^{4}y^{8}}}\) với \(x ≠ 0,\ y ≠ 0\).

a) So sánh \( \sqrt{25 - 16}\) và \(\sqrt {25}  - \sqrt {16}\);

b) Chứng minh rằng: với \(a > b >0\) thì \(\sqrt a  - \sqrt b  < \sqrt {a - b} \).

Tính

a) \( \sqrt{1\dfrac{9}{16}.5\dfrac{4}{9}.0,01}\);                    

b) \( \sqrt{1,44.1,21-1,44.0,4}\);

c) \( \sqrt{\dfrac{165^{2}-124^{2}}{164}}\);

d) \( \sqrt{\dfrac{149^{2}-76^{2}}{457^{2}-384^{2}}}\).

Giải phương trình 

a) \(\sqrt 2 .x - \sqrt {50}  = 0\);                  

b) \(\sqrt 3 .x + \sqrt 3  = \sqrt {12}  + \sqrt {27}\);

c) \(\sqrt 3 .{x^2} - \sqrt {12}  = 0\);

d) \(\dfrac{x^2}{\sqrt 5 } - \sqrt {20}  = 0\)

Rút gọn các biểu thức sau:

a) \( ab^{2}.\sqrt{\dfrac{3}{a^{2}b^{4}}}\) với \(a < 0,\ b ≠ 0\);

b) \( \sqrt{\dfrac{27(a - 3)^{2}}{48}}\) với \(a > 3\);

c) \( \sqrt{\dfrac{9+12a+4a^{2}}{b^{2}}}\) với \(a ≥ -1,5\) và \(b < 0.\)

d) \((a - b).\sqrt{\dfrac{ab}{(a - b)^{2}}}\) với \(a < b < 0\).

a) \(\sqrt {{{\left( {x - 3} \right)}^2}}  = 9\);

b) \(\sqrt {4{{\rm{x}}^2} + 4{\rm{x}} + 1}  = 6\).

Mỗi khẳng định sau đúng hay sai ? Vì sao ?

a) \(0,01 = \sqrt {0,0001} \);

b) \(- 0,5 = \sqrt { - 0,25} \);

c) \(\sqrt {39}  < 7\) và \(\sqrt {39}  > 6\);

d) \(\left( {4 - 13} \right).2{\rm{x}} < \sqrt 3 \left( {4 - \sqrt {13} } \right) \Leftrightarrow 2{\rm{x}} < \sqrt {3} \).

Đố: Trên lưới ô vuông, mỗi ô vuông cạnh \(1cm\), cho bốn điểm \(M,\ N,\ P,\ Q\) (h.3).

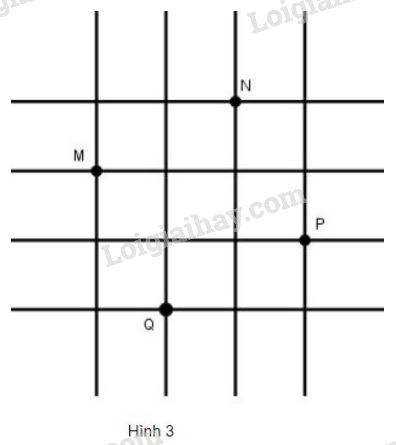
Hãy xác định số đo cạnh, đường chéo và diện tích của tứ giác \(MNPQ\).

Bài 1. Rút gọn :

a. \(A = \dfrac{{\sqrt {{x^2} - 10x + 25} }}{{x - 5}}\)

b. \(B = \left( {2x - y} \right).\sqrt {\dfrac{4}{{4{x^2} - 4xy + {y^2}}}} {\rm{ }}\)

Bài 2. Tìm x, biết:

a.\(\sqrt {\dfrac{8}{{x - 1}}}  = \sqrt 2 {\rm{ }}\) 

b. \(\dfrac{{\sqrt {{x^2} - 1} }}{{\sqrt {x - 1} }} = 2\)

Bài 3. Chứng minh rằng: 

\(\sqrt {\dfrac{{a + \sqrt {{a^2} - 1} }}{2}}  + \sqrt {\dfrac{{a - \sqrt {{a^2} - 1} }}{2}}  = \sqrt {a + 1} \;\left( {a > 1} \right)\)

Bài 1. Rút gọn :

a. \(A = {{\sqrt {8 - 2\sqrt {15} } } \over {\sqrt {10}  - \sqrt 6 }}\)

b. \(B = {1 \over {a{b^2}}}.\sqrt {{{{a^2}{b^4}} \over 3}} \)

Bài 2. Tìm x, biết : \({{\sqrt {x + 1} } \over {\sqrt {x - 1} }} = 2\)

Bài 3. Tìm x, biết : \(\sqrt {{{ - 1} \over {x - 1}}}  < 1\)

Bài 1. Rút gọn : \(A = \left( {{{\sqrt a } \over {\sqrt a  - 2}} + {{\sqrt a } \over {\sqrt a  + 2}}} \right):{{\sqrt {4a} } \over {a - 4}}\,\,\,\,\,\)\(\left( {a > 0;a \ne 4} \right)\)

Bài 2. Tìm x để biểu thức có nghĩa : \(M = \sqrt { - {5 \over {2x + 4}}} \)

Bài 3. Chứng minh : \(\left( {1 + {{a + \sqrt a } \over {\sqrt a  + 1}}} \right)\left( {1 - {{a - \sqrt a } \over {\sqrt a  - 1}}} \right) = 1 - a\,\,\,\,\)\(\left( {a \ge 0;a \ne 1} \right)\)

Bài 4. Tìm x, biết : \(\sqrt {{{x - 1} \over {x + 1}}}  = 2\)

Bài 1. Rút gọn : \(A = \left( {2 + {{x - 2\sqrt x  + 1} \over {1 - \sqrt x }}} \right).\left( {2 + {{x + 2\sqrt x  + 1} \over {\sqrt x  + 1}}} \right)\)\(\,\,\,\,\left( {x \ge 0;x \ne 1} \right)\)

Bài 2. Chứng minh rằng : \({{\sqrt {ab}  - b} \over b} - \sqrt {{a \over b}}  < 0\,\,\,\,\left( {a \ge 0;b > 0} \right)\)

Bài 3. Tìm x, biết : \({{\sqrt {2x - 1} } \over {\sqrt {x - 1} }} = 2\)

Bài 1. Rút gọn : \(A = \left( {{1 \over {\sqrt {1 + a} }} + \sqrt {1 - a} } \right):\left( {{1 \over {\sqrt {1 - {a^2}} }} + 1} \right)\)\(\,\,\,\,\left( { - 1 < a < 1} \right)\)

Bài 2. Tìm x, biết : \({{\sqrt {{x^2} - 4} } \over {\sqrt {x - 2} }} = 3\,\,\,\,\,\,\left( * \right)\)

Bài 3. Tìm giá trị nhỏ nhất của \(P = {{{x^2} + \sqrt x } \over {x - \sqrt x  + 1}} + 1 - {{2x + \sqrt x } \over {\sqrt x }}\,\,\,\,\,\left( {x > 0} \right)\)