Bài 2. Căn thức bậc hai và hằng đẳng thức
Bài Tập và lời giải
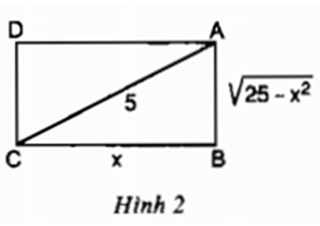
Hình chữ nhật ABCD có đường chéo AC = 5cm và cạnh BC = x (cm) thì cạnh \(AB = \sqrt {\left( {25 - {x^2}} \right)} \) (cm). Vì sao ? (h.2).
Với giá trị nào của \(x\) thì \( \sqrt {5-2x}\) xác định?
Với giá trị nào của \(a\) thì mỗi căn thức sau có nghĩa:
a) \( \sqrt{\dfrac{a}{3}}\), b) \(\sqrt{-5a}\); c) \( \sqrt{4 - a}\); d) \( \sqrt{3a + 7}\)
Tính
a) \(\sqrt {{{\left( {0,1} \right)}^2}}\) b) \(\sqrt {{{\left( { - 0,3} \right)}^2}}\)
c) \( - \sqrt {{{\left( { - 1,3} \right)}^2}} \) d) \( - 0,4\sqrt {{{\left( { - 0,4} \right)}^2}} \)
Rút gọn các biểu thức sau:
a) \(\sqrt {{{\left( {2 - \sqrt 3 } \right)}^2}} \) ; b) \(\sqrt {{{\left( {3 - \sqrt {11} } \right)}^2}} \)
c) \(2\sqrt {{a^2}} \) với a ≥ 0; d) \(3\sqrt {{{\left( {a - 2} \right)}^2}} \) với a < 2.
Tìm x biết:
a) \(\sqrt {{x^2}} = 7\) ;
b) \(\sqrt {{x^2}} = \left| { - 8} \right| \)
c) \(\sqrt {4{{\rm{x}}^2}} = 6\)
d) \(\sqrt {9{{\rm{x}}^2}} = \left| { - 12} \right|\);
Chứng minh
a) \((\sqrt{3}- 1)^{2}= 4 - 2\sqrt{3}\);
b) \(\sqrt{4 - 2\sqrt{3}}- \sqrt{3} = -1\)
Tính:
a) \(\sqrt{16}.\sqrt{25} + \sqrt{196}:\sqrt{49}\);
b) \(36:\sqrt{2.3^2.18}-\sqrt{169}\);
c) \(\sqrt{\sqrt{81}}\);
d) \( \sqrt{3^{2}+4^{2}}\).
Tìm x để mỗi căn thức sau có nghĩa:
a)\( \sqrt{2x + 7}\); c) \(\displaystyle \sqrt {{1 \over { - 1 + x}}} \)
b) \( \sqrt{-3x + 4}\) d) \( \sqrt{1 + x^{2}}\)
Rút gọn các biểu thức sau:
a) \(2\sqrt {{a^2}} - 5a\) với \(a < 0\).
b) \( \sqrt{25a^{2}}+ 3a\) với \(a ≥ 0\).
c) \(\sqrt {9{a^4}} + 3{a^2}\),
d) \( 5\sqrt{4a^{6}}\) - \( 3a^{3}\) với \(a < 0\)
Phân tích thành nhân tử:
a) \( x^{2}- 3\). b) \( x^{2}- 6\);
c) \( x^{2}\) + \( 2\sqrt{3}x + 3\); d) \( x^{2}\) - \( 2\sqrt{5}x + 5\).
Giải các phương trình sau:
a) \({x^2} - 5 = 0\); b) \({x^2} - 2\sqrt {11} x + 11 = 0\)
Đố. Hãy tìm chỗ sai trong phép chứng minh "Con muỗi nặng bằng con voi" dưới đây.
Giả sử con muỗi nặng \(m\) (gam), còn con voi nặng \(V\) (gam). Ta có
\({m^2} + {V^2} = {V^2} + {m^2}\)
Cộng hai về với \(-2mV\), ta có
\({m^2} - 2mV + {V^2} = {V^2} - 2mV + {m^2},\)
hay \({\left( {m - V} \right)^2} = {\left( {V - m} \right)^2}\)
Lấy căn bậc hai mỗi vế của bất đẳng thức trên, ta được:
\(\sqrt {{{\left( {m - V} \right)}^2}} = \sqrt {{{\left( {V - m} \right)}^2}} \) (1)
Do đó \(m - V = V - m\) (2)
Từ đó ta có \(2m = 2V\), suy ra \(m = V\). Vậy con muỗi nặng bằng con voi (!).
Bài 1. Tìm x để mỗi căn thức sau có nghĩa :
a. \(\sqrt {2x - 3} \)
b. \(\sqrt {{1 \over {2 - x}}} \)
c. \(\sqrt {x + 1} + \sqrt {1 - x} \)
Bài 2. Rút gọn các biểu thức :
a. \(\sqrt {9 - 4\sqrt 5 } - \sqrt 5 \)
b. \(\sqrt {3 - 2\sqrt 2 } - \sqrt {3 + 2\sqrt 2 } \)
Bài 1. Tìm x để mỗi biểu thức sau có nghĩa :
a. \(A = \sqrt {x - 3} - \sqrt {{1 \over {4 - x}}} \)
b. \(B = {1 \over {\sqrt {x - 1} }} + {2 \over {\sqrt {{x^2} - 4x + 4} }}\)
Bài 2. Rút gọn biểu thức : \(A = \sqrt {11 - 6\sqrt 2 } + 3 + \sqrt 2 \)
Bài 3. Tìm x, biết :
a. \(\sqrt {{x^2}} = 1\)
b. \(\sqrt {{x^2} - 2x + 1} = 2\)
Bài 1. Tìm x, biết :
a. \(\sqrt {{x^2} - 10x + 25} = 2\)
b. \(\sqrt {{x^2}} - 2x = 5\)
Bài 2. Chứng minh rằng : \(\sqrt {12 + 2\sqrt {11} } - \sqrt {12 - 2\sqrt {11} } = 2\)
Bài 1. Rút gọn : \(A = 3\sqrt 2 - \sqrt {6 - 4\sqrt 2 } \)
Bài 2. Cho biểu thức : \(P = \sqrt {9{x^2} - 6x + 1} + 1 - 4x\)
Tìm \(x > 1\) sao cho \(P = -4\)
Bài 3. Tìm x để biểu thức sau có nghĩa : \(\sqrt {{{ - 3} \over {x - 5}}} \)
Bài 1. Chứng minh rằng : \(\sqrt {x + 2\sqrt {x - 1} } + \sqrt {x - 2\sqrt {x - 1} } \) \( = 2\sqrt {x - 1} \), với x ≥ 2.
Bài 2. Rút gọn :
a. \(A = \left( {\sqrt 2 - 3} \right)\sqrt {11 + 6\sqrt 2 } \)
b. \(B = \sqrt {23 + 8\sqrt 7 } - \sqrt 7 \)
Bài 3. Tính giá trị của biểu thức :
\(A = - 4x + 2 + \sqrt {9{x^2} - 6x + 1} ,\) với \(x = 2009\).
