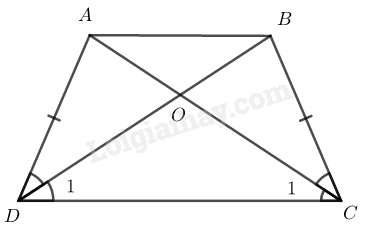
Xét \(∆ ADC\) và \(∆ BCD,\) ta có:
\(AD = BC\) (tính chất hình thang cân)
\(\widehat {ADC} = \widehat {BCD}\) \((gt)\)
\(DC\) cạnh chung
Do đó: \(∆ ADC = ∆ BCD\;\;\; (c.g.c)\)
\( \Rightarrow {\widehat C_1} = {\widehat D_1}\)
Trong \(∆ OCD\) ta có: \({\widehat C_1} = {\widehat D_1}\)
\(⇒ ∆ OCD\) cân tại \(O\)
\(⇒ OC = OD \;\;\;\;(1)\)
\(AC = BD\) ( tính chất hình thang cân)
\(⇒ AO + OC = BO + OD \;\;\;(2)\)
Từ \((1)\) và \((2)\) suy ra: \(AO = BO\)