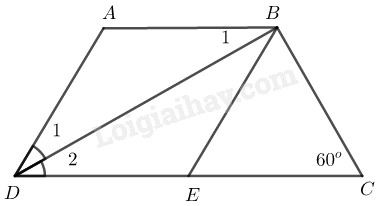
Hình thang \(ABCD\) cân có \(AB // CD\)
\( \Rightarrow \widehat D = \widehat C = {60^0}\)
\(DB\) là tia phân giác của góc \(D\)
\( \Rightarrow \widehat {D_1} = \widehat {D_2}=\dfrac{1}{2}\widehat D=30^0\)
Mà \(\widehat {B_1} = \widehat {D_2}\) (hai góc so le trong)
Suy ra: \(\widehat {D_1} = \widehat {B_1}\)
\(⇒ ∆ ABD\) cân tại \(A\) \(⇒ AB = AD\;\;\; (1)\)
Từ \(B\) kẻ đường thẳng song song với \(AD\) cắt \(CD\) tại \(E\)
Hình thang \(ABED\) có hai cạnh bên song song nên \(AB = ED,\) \(AD= BE\) \((2)\)
\(\widehat {BEC} = \widehat {ADC}\) (đồng vị )
Suy ra: \(\widehat {BEC} = \widehat C = {60^0}\)
\(⇒∆ BEC\) đều \(⇒ EC = BC \;\;\;(3)\)
\(AD = BC\) (tính chất hình thang cân) \((4)\)
Từ \((1),\) \((2),\) \((3)\) và \((4)\) \(⇒ AB = BC = AD = ED = EC\)
Chu vi hình thang \(ABCD\) bằng:
\(AB + BC + CD + AD \)\(= AB + BC + EC +ED +AD\)\( = 5AB\)
\(⇒AB = BC = AD = 20:5 = 4\;(cm)\)
\(CD = CE + DE = 2 AB \)\(= 2.4 = 8 \;\;(cm)\)