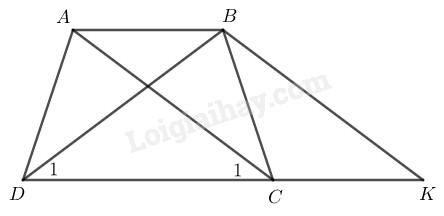
Từ \(B\) kẻ đường thẳng song song với \(AC\) cắt đường thẳng \(DC\) tại \(K.\)
Ta có hình thang \(ABKC\) có hai cạnh bên \(BK // AC\) nên \(AC = BK\)
Mà \(AC = BD \;\;\; (gt)\)
Suy ra: \(BD = BK\) do đó \(∆ BDK\) cân tại \(B\)
\( \Rightarrow {\widehat D_1} = \widehat K\) (tính chất tam giác cân)
Ta lại có: \({\widehat C_1} = \widehat K\) (hai góc đồng vị)
Suy ra: \({\widehat D_1} = {\widehat C_1}\)
Xét \(∆ ACD\) và \(∆ BDC:\)
\(AC = BD \;\;\; (gt)\)
\({\widehat D_1} = {\widehat C_1}\) (chứng minh trên)
\(CD\) cạnh chung
Do đó: \(∆ ACD = ∆ BDC\;\;\; (c.g.c)\) \( \Rightarrow \widehat {ADC} = \widehat {BCD}\)
Hình thang \(ABCD\) có \(\widehat {ADC} = \widehat {BCD}\) nên là hình thang cân.