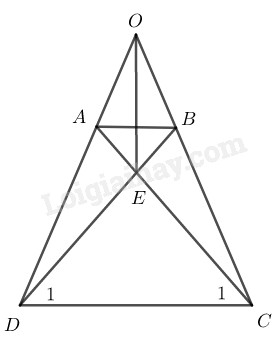
\(\eqalign{
& \widehat {ADC} = \widehat {BCD}\,\,\,\,(gt) \cr
& \Rightarrow \widehat {ODC} = \widehat {OCD} \cr} \)
\(⇒ ∆ OCD\) cân tại \(O\)
\(⇒ OC = OD\)
\(⇒ OA + AD = OB + BC\)
Mà \(AD = BC\) (tính chất hình thang cân)
\(⇒ OA = OB\)
Xét \(∆ ADC\) và \(∆ BCD :\)
\(AD = BC\) (chứng minh trên)
\(AC = BD\) (tính chất hình thang cân)
\(CD\) cạnh chung
Do đó: \(∆ ADC = ∆ BCD\;\;\; (c.c.c)\)
\( \Rightarrow {\widehat D_1} = {\widehat C_1}\)
\(⇒ ∆ EDC\) cân tại \(E\)
\(⇒ EC = ED\) nên \(E\) thuộc đường trung trực của \(CD\)
\(OC = OD\) nên \(O\) thuộc đường trung trực của \(CD\)
\(E≢ O.\) Vậy \(OE\) là đường trung trực của \(CD.\)
\(BD = AC\) (tính chất hình thang cân)
\(⇒ EB + ED = EA + EC\) mà \(ED = EC\) (chứng minh trên)
\(⇒ EB = EA\) \(\Rightarrow \Delta EAB\) cân tại \(E\)
nên \(E\) thuộc đường trung trực \(AB\)
\( OA = OB\) ( chứng minh trên) \(\Rightarrow \Delta OAB\) cân tại \(O\)
nên \(O\) thuộc đường trung trực \(AB\)
\(E≢ O.\) Vậy \(OE\) là đường trung trực của \(AB.\)