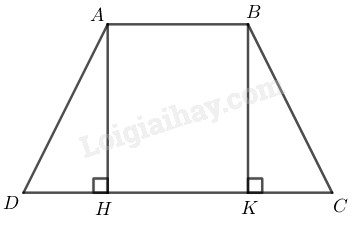
\(a)\) Kẻ đường cao \(BK\)
Xét hai tam giác vuông \(AHD\) và \(BKC,\) ta có:
\(\widehat {AHB} = \widehat {BKC} = {90^0}\)
\(AD = BC\) (tính chất hình thang cân)
\(\widehat D = \widehat C\) (gt)
Do đó: \(∆ AHD = ∆ BKC\) (cạnh huyền- góc nhọn)
\(⇒ HD = KC\)
Ta có: \(AH//BK\) (cùng vuông góc với \(CD\))
Hình thang \(ABKH\) có hai cạnh bên \(AH,\;BK\) song song nên \(AB = HK\)
\(a−b = DC – AB = DC – HK\)\( = HD + KC = 2HD\)
\( \Rightarrow HD =\displaystyle {{a - b} \over 2}\)
\(HC = DC-HD = a - \displaystyle{{a - b} \over 2}\)\( = \displaystyle{{a + b} \over 2}\)
\( b)\) \(HD = \displaystyle{{CD - AB} \over 2}\)\( = \displaystyle{{26 - 10} \over 2} = 8\left( {cm} \right)\)
Trong tam giác vuông \(AHD\) có \(\widehat {AHD} = {90^0}\)
\(A{D^2} = A{H^2} + H{D^2}\) (định lí Py-ta-go)
\(\eqalign{
& \Rightarrow A{H^2} = A{D^2} - H{D^2} \cr
& \Rightarrow A{H^2} = {17^2} - {8^2} = 289 - 64 = 225 \cr
& \Rightarrow AH = 15(cm) \cr} \)