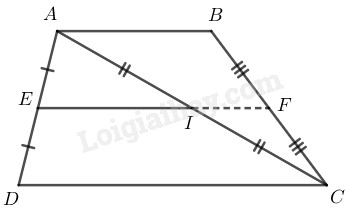
Hình thang \(ABCD\) có \(AB// CD\)
\(E\) là trung điểm của \(AD \;\;(gt)\)
\(F\) là trung điểm của \(BC\;\; (gt)\)
Nên \(EF\) là đường trung bình của hình thang \(ABCD\)
\(⇒ EF // CD\) (tính chất đường trung bình hình thang) \((1)\)
Trong \(∆ ADC\) có:
\(E\) là trung điểm của \(AD \;\;(gt)\)
\(I\) là trung điểm của \(AC\;\; (gt)\)
Nên \(EI\) là đường trung bình của \(∆ ADC\)
\(⇒ EI // CD\) (tính chất đường trung bình tam giác) \((2)\)
Từ \((1)\) và \((2)\) theo tiên đề Ơclít đường thẳng \(EF\) và \(EI\) trùng nhau
Vậy \(E, I, F\) thẳng hàng.