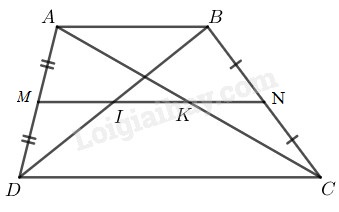
Hình thang \(ABCD\) có \(AB // CD\)
\(M\) là trung điểm của \(AD\;\; (gt)\)
\(N\) là trung điểm của \(BC\;\; (gt)\)
Nên \(MN\) là đường trung bình của hình thang \(ABCD\)
\(⇒ MN // AB // CD\)
\(MN =\displaystyle {{AB + CD} \over 2} = {{6 + 14} \over 2} = 10\left( {cm} \right)\)
Trong tam giác \(ADC\) ta có:
\(M\) là trung điểm của \(AD\)
\(MK // CD\)
\(⇒ AK = KC\) và \(MK\) là đường trung bình của \(∆ ADC.\)
\( \Rightarrow MK = \displaystyle {1 \over 2}CD = {1 \over 2}.14 = 7\left( {cm} \right)\)
Vậy: \(KN = MN – MK = 10 – 7 = 3 \;\;(cm)\)
Trong \(∆ ADB\) ta có:
\(M\) là trung điểm của \(AD\)
\(MI // AB\) nên \(DI = IB\)
\(⇒ MI\) là đường trung bình của \(∆ DAB\)
\( \Rightarrow MI =\displaystyle {1 \over 2}AB = {1 \over 2}.6 = 3\left( {cm} \right)\)
\(IK = MK – MI = 7 – 3 = 4\;\; (cm)\)