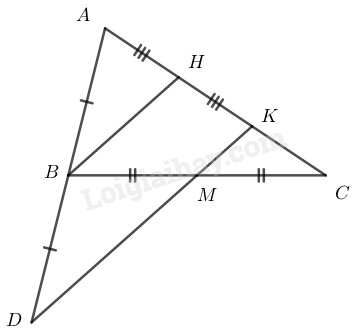
Gọi \(H\) là trung điểm của \(AK\)
Trong \(∆ ADK\) ta có:
\(H\) là trung điểm của \(AK\)
\(B\) là trung điểm của \(AD\) ( \(AB=BD\))
\(\Rightarrow BH\) là đường trung bình của \(∆ ADK.\)
\(⇒ BH // DK\) (tính chất đường trung bình của tam giác)
Hay \(BH // MK\)
Trong \(∆ BCH\) ta có \(M\) là trung điểm của \(BC\)
\(MK // BH\)
\(⇒ CK = HK\)
\(AK = AH + HK = 2HK\)
Suy ra: \(AK = 2 CK.\)