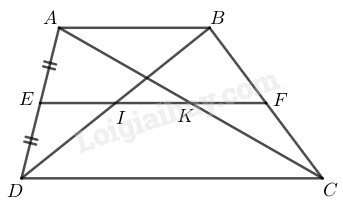
Xét hình thang \(ABCD\) có: \(AB // CD.\)
\(E\) là trung điểm của \(AD,\) đường thẳng đi qua \(E\) song song với \(AB\) cắt \(BC\) tại \(F,\) \(AC\) tại \(K,\) \(BD \) tại \(I.\)
Vì \(E\) là trung điểm của \(AD\)
\(EF // AB\)
Suy ra: \(BF = FC\) (tính chất đường trung bình hình thang)
Trong tam giác \(ADC\) ta có:
\(E\) là trung điểm của \(AD\)
\(EK // DC\)
Suy ra: \(AK = KC\) (tính chất đường trung bình tam giác)
Trong tam giác \(ABD\) ta có:
\(E\) là trung điểm cạnh \(AD\)\(EI // AB\)
Suy ra: \(BI = ID\) (tính chất đường trung bình của tam giác)
Vậy đường thẳng đi qua trung điểm \(E\) của cạnh bên \(AD\) của hình thang \(ABCD\) thì đi qua trung điểm cạnh bên \(BC\) và trung điểm hai đường chéo \(AC, BD.\)