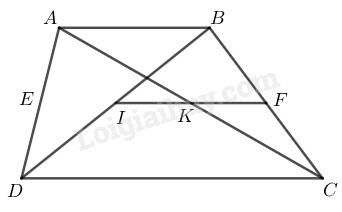
Giả sử hình thang \(ABCD\) có \(AB // CD,\) \(AB < CD.\)
\(I, K\) lần lượt là trung điểm hai đường chéo \(BD, AC\)
Gọi \(F\) là trung điểm của \(BC\)
Trong tam giác \(ACB\) ta có:
\(K\) là trung điểm của cạnh \(AC\)
\(F\) là trung điểm của cạnh \(BC\)
Nên \(KF\) là đường trung bình của \(∆ ABC\)
\(⇒ KF // AB\) và \(KF = \displaystyle{1 \over 2}AB\) (tính chất đường trung bình của tam giác)
Trong tam giác \(BDC\) ta có:
\(I\) là trung điểm của cạnh \(BD\)
\(F\) là trung điểm của cạnh \(BC\)
Nên \(IF\) là đường trung bình của \(∆ BDC\)
\(⇒ IF // CD\) và \(IF = \displaystyle {1 \over 2}CD\) (tính chất đường trung bình của tam giác)
\(FK // AB\) mà \(AB // CD\) nên \(FK // CD\)
\(FI // CD\) (chứng minh trên)
Suy ra hai đường thẳng \(FI\) và \(FK\) trùng nhau.
\(⇒ I, K, F\) thẳng hàng, \(AB < CD\)\( ⇒ FK < FI\) nên \(K\) nằm giữa \(I\) và \(F\)
\(IF = IK + KF\)
\(\eqalign{
& \Rightarrow IK = IF - KF \cr
& = \displaystyle{1 \over 2}CD - {1 \over 2}AB = {{CD - AB} \over 2} \cr} \)