Bài 5.1, 5.2 phần bài tập bổ sung trang 15 SBT toán 9 tập 2

Bài 5.1

Tổng số tuổi của tôi và của em tôi năm nay bằng \(26\). Khi tổng số tuổi của chúng tôi gấp \(5\) lần tuổi của tôi hiện nay thì tuổi của tôi khi đó sẽ gấp \(3\) lần tuổi của em tôi hiện nay. Hãy tính tuổi hiện nay của mỗi người chúng tôii

Phương  pháp:

Sử dụng

- Cách giải bài toán bằng cách lập hệ hai phương trình bậc nhất hai ẩn :

Bước 1: Lập hệ phương trình

+ Chọn hai ẩn và đặt điều kiện thích hợp cho chúng

+ Biểu diễn các đại lượng chưa biết theo các ẩn và các đại lượng đã biết

+ Lập hai phương trình biểu thị mối quan hệ giữa các đại lượng.

Bước 2: Giải hệ phương trình nói trên.

Bước 3: Kiểm tra xem trong các nghiệm của hệ phương trình, nghiệm nào thích hợp với bài toán và kết luận.

Gọi tuổi của tôi hiện nay là \(x\) (tuổi), điều kiện: \(x \in {\mathbb{N}^*}\)

Tổng số tuổi của tôi và của em tôi năm nay bằng \(26\) nên tuổi của em tôi hiện nay là \(26 – x\) (tuổi)

Gọi số năm phải thêm là \(y\) (năm), điều kiện: \(y \in {\mathbb{N}^*}\)

Vì sau \(y\) năm tổng số tuổi của chúng tôi gấp \(5\) lần tuổi của tôi hiện nay nên ta có phương trình:

\(\left( {x + y} \right) + \left( {26 - x + y} \right) = 5x\)

Tuổi của tôi sau \(y\) năm gấp \(3\) lần tuổi của em tôi hiện nay nên ta có phương trình:

\(x + y = 3\left( {26 - x} \right)\)

Khi đó ta có hệ phương trình:

\(\eqalign{
& \left\{ {\matrix{
{\left( {x + y} \right) + \left( {26 - x + y} \right) = 5x} \cr 
{x + y = 3\left( {26 - x} \right)} \cr
} } \right. \cr 
& \Leftrightarrow \left\{ {\matrix{
{5x - 2y = 26} \cr 
{4x + y = 78} \cr
} } \right. \cr& \Leftrightarrow \left\{ {\matrix{
{5x - 2y = 26} \cr 
{8x + 2y = 156} \cr
} } \right. \cr 
& \Leftrightarrow \left\{ {\matrix{
{13x = 182} \cr 
{4x + y = 78} \cr
} } \right. \cr& \Leftrightarrow \left\{ {\matrix{
{x = 14} \cr 
{4.14 + y = 78} \cr
} } \right. \cr 
& \Leftrightarrow \left\{ {\matrix{
{x = 14} \cr 
{y = 22} \cr} } \right. \cr} \)

Ta thấy \(x = 14; y = 22\) thỏa mãn điều kiện bài toán.

Vậy hiện nay tuổi của tôi là \(14\) tuổi, tuổi của em tôi là \(26 – 14 = 12\) (tuổi).

Bài 5.2

Có hai bến xe khách \(P\) và \(Q\). Một người đi xe đạp từ \(P\) đến \(Q\) với vận tốc không đổi, nhận thấy cứ \(15\) phút lại có một xe khách đi cùng chiều vượt qua và cứ \(10\) phút lại gặp một xe khách đi ngược chiều. Giả thiết rằng các xe khách chạy với cùng một vận tốc, không dừng lại trên đường và ở cả hai bến, cứ \(x\) phút lại có một xe rời bến. Hỏi thời gian \(x\) là bao nhiêu phút và vận tốc xe khách bằng bao nhiêu lần vận tốc người đi xe đạp?

Phương pháp:

Sử dụng:

- Cách giải bài toán bằng cách lập hệ hai phương trình bậc nhất hai ẩn :

Bước \(1\): Lập hệ phương trình

+ Chọn hai ẩn và đặt điều kiện thích hợp cho chúng

+ Biểu diễn các đại lượng chưa biết theo các ẩn và các đại lượng đã biết

+ Lập hai phương trình biểu thị mối quan hệ giữa các đại lượng.

Bước \(2\): Giải hệ phương trình nói trên.

Bước \(3\): Kiểm tra xem trong các nghiệm của hệ phương trình, nghiệm nào thích hợp với bài toán và kết luận.

- Công thức tính quãng đường đi được: \(S=v.t;\)

Trong đó \(S\) là quãng đường đi được \((km)\); \(v\) là vận tốc \((km/h)\); \(t\) là thời gian \((h)\).

Gọi vận tốc người đi xe đạp là \(y\) (km/phút), vận tốc xe khách là \(z\) (km/phút)

Điều kiện: \(z > y > 0\)

- Xét trường hợp các xe khách đi cùng chiều với người đi xe đạp.

Giả sử khi xe khách thứ nhất vượt người đi xe đạp tại điểm \(B\) thì xe khách thứ hai ở điểm \(A\) như hình vẽ.

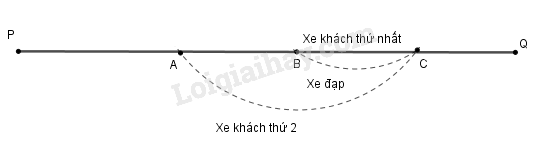
Hai xe khách khởi hành cách nhau \(x\) phút nên quãng đường \(AB\) là quãng đường mà xe khách phải đi trong \(x\) phút và \( AB = xz \) (km).

Gọi điểm mà xe khách thứ hai vượt người đi xe đạp là \(C\) thì quãng đường \(BC\) là quãng đường người đi xe đạp đi trong \(15\) phút nên \( BC=15y\) (km). Quãng đường \(AC\) là quãng đường xe khách đi trong \(15\) phút nên \(AC =15z\) (km).

Ta có phương trình: \(xz + 15y = 15z\)

- Xét trường hợp các xe khách đi ngược chiều với người đi xe đạp.

Giả sử người đi xe đạp gặp xe khách thứ nhất đi ngược chiều tại điểm \(D\) thì xe khách thứ hai đi ngược chiều  đang ở vị trí \(E\) như hình vẽ.

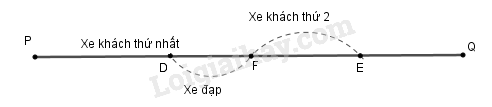
Hai xe khách khởi hành cách nhau \(x\) phút nên \(DE= xz\) (km). Sau đó \(10\) phút, người đi xe đạp gặp xe khách thứ hai tại điểm \(F\). Khi đó, quãng đường \(DF\) là quãng đường người đi xe đạp đi trong \(10\) phút nên \( DF=10y\) (km). Quãng đường \(EF\) là quãng đường xe khách đi trong \(10\) phút nên \(EF =10z\) (km).

Ta có phương trình:  \(10y + 10z = xz\)

Ta có hệ phương trình:

\(\eqalign{
& \left\{ {\matrix{
{xz + 15y = 15z} \cr 
{10y + 10z = xz} \cr
} } \right. \cr& \Leftrightarrow \left\{ {\matrix{
{xz + 15y = 15z} \cr 
{xz - 10y = 10z} \cr
} } \right. \cr 
& \Leftrightarrow \left\{ {\matrix{
{x + \displaystyle 15.{y \over z} = 15} \cr 
{x -  \displaystyle10.{y \over z} = 10} \cr} } \right. \cr} \)

Đặt \( \displaystyle{y \over z} = t\) \((t>0)\)

Khi đó hệ phương trình trên trở thành:

\(\eqalign{
& \left\{ {\matrix{
{x + 15t = 15} \cr 
{x - 10t = 10} \cr
} } \right. \Leftrightarrow \left\{ {\matrix{
{25t = 5} \cr 
{x - 10t = 10} \cr
} } \right. \cr 
& \Leftrightarrow \left\{ {\matrix{
{t =  \displaystyle{1 \over 5}}  \text {(thoả mãn)}\cr 
{x - 10t = 10} \cr
} } \right. \cr 
&\Leftrightarrow \left\{ {\matrix{
{t =  \displaystyle{1 \over 5}} \cr 
{x - 10. \displaystyle{1 \over 5} = 10} \cr
} } \right. \cr& \Leftrightarrow \left\{ {\matrix{
{t = \displaystyle {1 \over 5}} \cr 
{x = 12} \cr} } \right. \cr} \)

Suy ra: \(x = 12; \displaystyle{y \over z} = {1 \over 5} \Rightarrow 5y = z\)

Vậy cứ \(12\) phút lại có một chuyến xe khách rời bến và vấn tốc của xe khách gấp \(5\) lần vận tốc của người đi xe đạp.