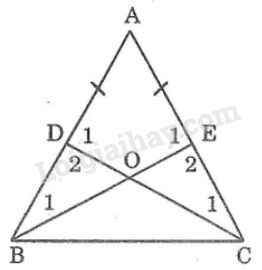
a) Xét \(∆BEA\) và \(∆CDA\) có:
\(BA = CA\) (gt)
\(\widehat A\) chung
\(AE = AD\) (gt)
\(\Rightarrow ∆BEA = ∆CDA\) (c.g.c)
\(\Rightarrow BE = CD\) (hai cạnh tương ứng)
b) \(∆BEA = ∆CDA\) (chứng minh trên)
\(\Rightarrow \widehat {{B_1}} = \widehat {{C_1}};\widehat {{E_1}} = \widehat {{D_1}}\) (hai góc tương ứng) (1)
\(\widehat {{E_1}} + \widehat {{E_2}} = 180^\circ \) (hai góc kề bù) (2)
\(\widehat {{D_1}} + \widehat {{D_2}} = 180^\circ \) (hai góc kề bù) (3)
Từ (1), (2) và (3) \( \Rightarrow \widehat {{E_2}} = \widehat {{D_2}}\)
\(AB = AC\) (gt)
\( \Rightarrow AE + EC = AD + DB\) mà \(AE = AD\) (gt) \( \Rightarrow EC = DB\)
Xét \(∆ODB\) và \(∆OEC\) có:
\(\widehat {{D_2}} = \widehat {{E_2}}\) (chứng minh trên)
\(DB = EC\) (chứng minh trên)
\(\widehat {{B_1}} = \widehat {{C_1}}\) (chứng minh trên)
\( \Rightarrow ∆ODB = ∆OEC \) (g.c.g)