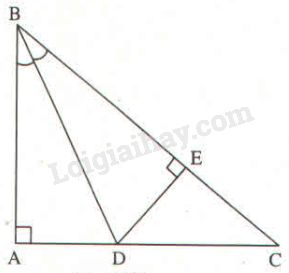
Xét hai tam giác vuông \(ABD\) và \(EBD,\) có:
\(\widehat {BA{\rm{D}}} = \widehat {BE{\rm{D}}} = 90^\circ \)
Cạnh huyền \(BD\) chung
\(\widehat {AB{\rm{D}}} = \widehat {EB{\rm{D}}}\) (vì \(BD\) là phân giác góc \(B\) )
\( \Rightarrow ∆ABD = ∆EBD\) (cạnh huyền góc nhọn)
\( \Rightarrow BA = BE\) (hai cạnh tương ứng).