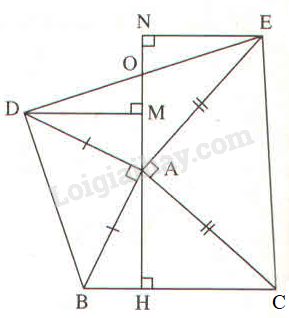
a) Ta có \(\widehat {BAH} + \widehat {BA{\rm{D}}} + \widehat {DAM} = 180^\circ \)
Mà \(\widehat {BA{\rm{D}}} = 90^\circ \Rightarrow \widehat {BAH} + \widehat {DAM} = 90^\circ \) (1)
Xét tam giác \(AMD\) có \(\widehat {AM{\rm{D }}} = 90^\circ\)
\( \Rightarrow \widehat {DAM} + \widehat {A{\rm{D}}M} = 90^\circ \left( 2 \right)\)
Từ (1) và (2) suy ra: \(\widehat {BAH} = \widehat {A{\rm{D}}M}\)
Xét hai tam giác vuông \(AMD\) và \(BHA\) có:
\(\widehat {AM{\rm{D}}} = \widehat {BHA} = 90^\circ \)
\( DA=AB \) (gt)
\( \widehat {A{\rm{D}}M}=\widehat {BAH} \) (chứng minh trên)
\( \Rightarrow ∆AMD = ∆BHA \) (cạnh huyền, góc nhọn)
\( \Rightarrow DM=AH \) (hai cạnh tương ứng) (3)
b) Ta có: \(\widehat {HAC} + \widehat {CA{\rm{E}}} + \widehat {N{\rm{A}}E} = 180^\circ \)
Mà \(\widehat {CA{\rm{E}}} = 90^\circ \left( {gt} \right) \)
\(\Rightarrow \widehat {HAC} + \widehat {N{\rm{A}}E} = 90^\circ \) (4)
Xét tam giác \(AHC\) có \(\widehat {AHC} = 90^\circ \)
\(\Rightarrow \widehat {HAC} + \widehat {HCA} = 90^\circ\;\; \left( 5 \right)\)
Từ (4) và (5) suy ra: \(\widehat {HCA} = \widehat {N{\rm{A}}E}\)
Xét hai tam giác vuông \(AHC\) và \(ENA\) có:
\(\widehat {AHC} = \widehat {E{\rm{N}}A} = 90^\circ \)
\(AC = EA\) (gt)
\(\widehat {HCA} = \widehat {N{\rm{A}}E}\) (chứng minh trên)
\( \Rightarrow ∆AHC = ∆ENA\) (cạnh huyền, góc nhọn)
\( \Rightarrow AH = EN\) (hai cạnh tương ứng) (6)
Từ (3) và (6) suy ra: \(DM = EN\).
Vì \(DM \bot AH\) và \(EN \bot AH\) nên \(DM // EN\) (hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng song song với nhau)
Gọi \(O\) là giao điểm của \(MN\) và \(DE\)
Vì \(MN//DE\) nên \(\widehat {M{\rm{D}}O} = \widehat {NEO}\) (cặp góc so le trong).
Xét hai tam giác vuông \(DMO\) và \(ENO\) có:
\(\widehat {DMO} = \widehat {EN{\rm{O}}} = 90^\circ \)
\(DM = EN\) (chứng minh trên)
\(\widehat {M{\rm{D}}O} = \widehat {NEO}\) (chứng minh trên)
\( \Rightarrow ∆DMO = ∆ENO \) (g.c.g)
\( \Rightarrow OD = OE\) (hai cạnh tương ứng).
\(\Rightarrow O\) là trung điểm của \(DE\).
Vậy \(MN\) đi qua trung điểm của \(DE.\)