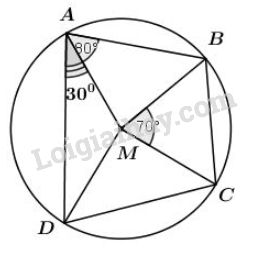
Ta có: \(\widehat {MAB} = \widehat {DAB} - \widehat {DAM} = {80^0} - {30^0} = {50^0}\) (1)
+) \(∆MBC\) là tam giác cân cân tại \(M\) \((MB= MC)\) nên \(\displaystyle \widehat {BCM} = {{{{180}^0} - {{70}^0}} \over 2} = {55^0}\) (2)
+) \(∆MAB\) là tam giác cân tại \(M\) \((MA=MB)\) nên \(\widehat {MAB} =\widehat {ABM} = {50^0}\) (theo (1))
Vậy \(\widehat {AMB} = {180^0} - {2.50^0} = {80^0}.\)
Ta có: \(\widehat {BAD}=\dfrac{sđ\overparen{BCD}}{2}\) (số đo góc nội tiếp bằng nửa số đo của cung bị chắn).
\(\Rightarrow sđ\overparen{BCD}=2.\widehat {BAD} = {2.80^0} = {160^0}.\)
Mà \(sđ\overparen{BC}= \widehat {BMC} = {70^0}\) (số đo góc ở tâm bằng số đo cung bị chắn).
Vậy \(sđ\overparen{DC}={160^0} - {70^0} = {90^0}\) (vì C nằm trên cung nhỏ cung \(BD\)).
Suy ra \(\widehat {DMC} = {90^0}.\) (4)
Ta có: \(∆MAD\) là tam giác cân cân tại \(M \) \((MA= MD).\)
Suy ra \(\widehat {AMD} = {180^0} - {2.30^0}=120^0\) (5)
Có \(∆MCD\) là tam giác vuông cân tại \(M\) \((MC= MD)\) và \(\widehat {DMC} = {90^0}\)
Suy ra \(\widehat {MCD} = \widehat {MDC} = {45^0}.\) (6)
Theo (2) và (6) và vì CM là tia nằm giữa hai tia \(CB, \, CD\) ta có: \(\widehat {BCD} =\widehat{BCM}+\widehat{MCD} ={100^0}.\)