* Hình bình hành nói chung không nội tiếp được đường tròn vì tổng hai góc đối diện không bằng \(180^0\).
* Trường hợp riêng của hình bình hành là hình chữ nhật (hay hình vuông) thì nội tiếp đường tròn vì tổng hai góc đối diện là \(90^0 + 90^0= 180^0.\)
* Hình thang nói chung và hình thang vuông không nội tiếp được đường tròn.
* Hình thang cân \(ABCD \, (BC= AD)\) có hai góc ở mỗi đáy bằng nhau: \(\widehat{A}= \widehat{B},\) \(\widehat{C} =\widehat{D}\)
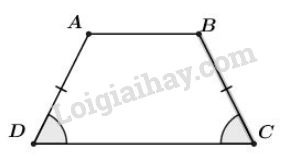
Vì \(AD // CD\) nên \(\widehat{A} +\widehat{D} = 180^0\) (hai góc trong cùng phía), suy ra \(\widehat{A} +\widehat{C} =180^0\).
Vậy hình thang cân luôn có tổng hai góc đối diện bằng \(180^0\) nên là tứ giác nội tiếp.