Đề kiểm tra 15 phút - Đề số 2 - Bài 4 - Chương 2 - Đại số 8
Lời giải
Bài Tập và lời giải
Giải câu 2 trang 58 SBT địa 6
Dựa vào kiến thức đã học và hình 18-1, hãy cho biết:- Cứ lên cao 100 m nhiệt độ lại giảm bao nhiêu độ.- Nếu địa điểm A có độ cao là 0 m, hãy cho biết địa điểm B có độ cao là bao nhiêu mét.

Giải câu 3 trang 59 SBT địa 6
Đề bài
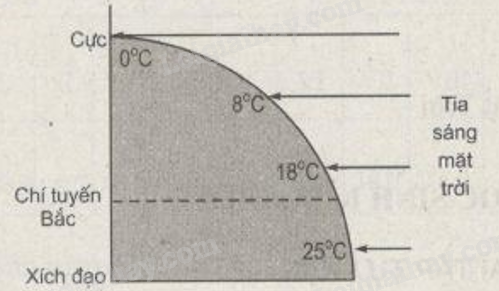
Dựa vào hình 18-2, hãy:
- Nhận xét sự thay đổi nhiệt độ theo vĩ độ.
- Giải thích vì sao nhiệt độ có sự thay đổi như vậy.