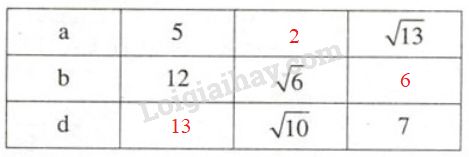
Cột thứ hai:
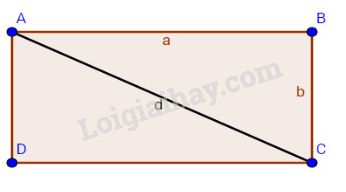
Áp dụng định lí Pytago vào tam giác vuông \(ABC\) có \( \widehat {ABC} = {90^o}\) ta có:
\({d^{2}} = {\rm{ }}{a^2} + {\rm{ }}{b^2} = {\rm{ }}{5^2} + {\rm{ }}{12^2} = {\rm{ }}25{\rm{ }} + {\rm{ }}144{\rm{ }}\)\( = {\rm{ }}169\)
Nên \(d =\sqrt{169}= 13\)
Cột thứ ba:
Áp dụng định lí Pytago vào tam giác vuông \(ABC\) có \( \widehat {ABC} = {90^o}\) ta có:
\({a^2} + {\rm{ }}{b^{2}} = {d^2} \)
\(\Rightarrow {a^2} = {\rm{ }}{d^2} - {b^2} = {\left( {\sqrt {10} } \right)^2} - {\left( {\sqrt 6 } \right)^2}\)
\(= 10 - 6 = 4\Rightarrow a = \sqrt 4=2\)
Cột thứ tư:
Áp dụng định lí Pytago vào tam giác vuông \(ABC\) có \( \widehat {ABC} = {90^o}\) ta có:
\({a^2} + {\rm{ }}{b^{2}} = {\rm{ }}{d^2}\)
\(\Rightarrow {b^2} = {\rm{ }}{d^2} - {\rm{ }}{a^2} = {\rm{ }}{7^2} -{\left( {\sqrt {13} } \right)^2}\)
\(= 49 - 13 = 36\Rightarrow b=\sqrt {36}= 6\)