Đề kiểm tra 15 phút - Đề số 10 - Bài 9, 10 - Chương 1 - Hình học 8

Cho hình chữ nhật ABCD. Gọi O là giao điểm của hai đường chéo AC và BD. Lấy E nằm giữa hai điểm O và B. Gọi F là điểm đối xứng với điểm A qua E và I là trung điểm của CF.

a) Chứng minh tứ giác OEFC là hình thang và tứ giác OEIC là hình bình hành.

b) Gọi H và K lần lượt là hình chiếu của điểm F trên các đường thẳng BC và CD. Chứng minh tứ giác CHFK là hình chữ nhật và I là trung điểm của đoạn HK.

c) Chứng minh ba điểm E, H, K thẳng hàng.

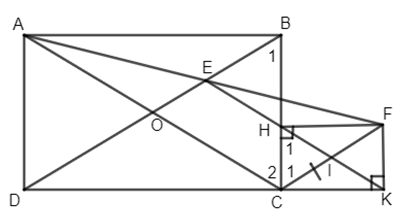
a) Ta có EA = EF (tính chất đối xứng)

 OA = OC (tính chất hai đường chéo của hình chữ nhật)

\( \Rightarrow OE\) là đường trung bình của \(\Delta ACF \Rightarrow OE//CF.\)

b) Ta có \(FH \bot BC\) hay \(\widehat {FHC} = {90^ \circ },\widehat {HCK} = {90^ \circ },\)\(\;\widehat {FKC} = {90^ \circ }(gt)\)

c) Ta có \(\Delta HIC\) cân (tính chất đường chéo hình chữ nhât) \( \Rightarrow \widehat C_1= \widehat H_1\)

Tương tự \(\Delta COB\) cân \( \Rightarrow \widehat B_1 = \widehat C_2 \) mà \(OE// CF \Rightarrow \widehat B_1 = \widehat C_1\) (so le trong)

\( \Rightarrow \widehat C_2 = \widehat H_1 \Rightarrow HI//AC.\)

Lại có \(EI//OC\) (vì OEIC là hình bình hành) \( \Rightarrow EI\) và HI phải trùng nhau hay ba điểm E, H, I thẳng hàng \( \Rightarrow \) Ba điểm E, H, K thẳng hàng.