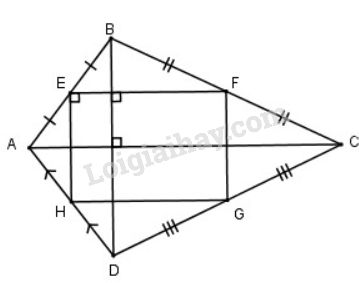
Vì \(E,F\) lần lượt là trung điểm của \(AB,BC\) (giả thiết)
\( \Rightarrow \) \(EF\) là đường trung bình của \(∆ABC\) (dấu hiệu nhận biết đường trung bình của tam giác)
\( \Rightarrow \) \(EF // AC\) (1) (tính chất đường trung bình của tam giác)
Do \(G,H\) lần lượt là trung điểm của \(CD,DA\) (giả thiết)
\( \Rightarrow \) \( HG\) là đường trung bình của \(∆ADC\) (dấu hiệu nhận biết đường trung bình của tam giác)
\( \Rightarrow \) \(HG // AC\) (2) (tính chất đường trung bình của tam giác)
Từ (1) và (2) \( \Rightarrow \) \(EF // HG\).
Vì \(E,H\) lần lượt là trung điểm của \(AB,AD\) (giả thiết)
\( \Rightarrow \) \(EH\) là đường trung bình của \(∆ABD\) (dấu hiệu nhận biết đường trung bình của tam giác)
\( \Rightarrow \) \(EH // BD\) (3) (tính chất đường trung bình của tam giác)
Do \(G,F\) lần lượt là trung điểm của \(CD,BC\) (giả thiết)
\( \Rightarrow \) \( GF\) là đường trung bình của \(∆BDC\) (dấu hiệu nhận biết đường trung bình của tam giác)
\( \Rightarrow \) \(GF // BD\) (4) (tính chất đường trung bình của tam giác)
Từ (3) và (4) \( \Rightarrow \) \(GF // EH\).
\( \Rightarrow \) \(EFGH\) là hình bình hành (dấu hiệu nhận biết hình bình hành)
Ta có: \(EF // AC\) và \(EH//BD\) mà \(AC\bot BD\) nên \(EF\bot EH\)
Hay \(\widehat{FEH} = 90^0\)
Hình bình hành \(EFGH\) có \(\widehat{E} = 90^0\) nên là hình chữ nhật (theo dấu hiệu nhận biết hình chữ nhật).