Đề kiểm tra 15 phút - Đề số 1 - Bài 7 - Chương 1 - Hình học 8
Cho tam giác ABC, hai trung tuyến BM, CN cắt nhau tại G. Gọi E, F lần lượt là trung điểm của GB và GC.
a)Chứng minh tứ giác MNEF là hình bình hành.
b)Lấy I, J thuộc tia đối của MG và NG sao cho MI = MG và NI = NG. Chứng minh tứ giác BCIJ là hình bình hành.
Lời giải
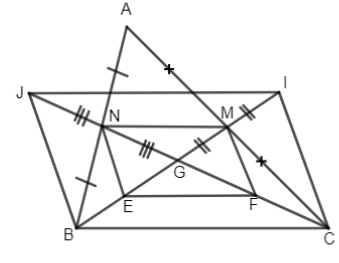
a) Ta có MN là đường trung bình của \(\Delta ABC\)
\( \Rightarrow MN//BC\) và \(MN = \dfrac{1}{ 2}BC.\)
Tương tự EF là đường trung bình của \(\Delta BGC\) nên \({\rm{EF}}// BC\) và \({\rm{EF}} = \dfrac{1}{ 2}BC.\)
Do đó \(MN// {\rm{EF}}\) và \(MN = EF.\)
Vậy MNEF là hình bình hanh (hai cạnh đối vừa song song vừa bằng nhau).
b) Ta có G là trọng tâm của \(\Delta ABC\) nên \(GN = \dfrac{1 }{ 2}GC\)
mà GN = JN (gt) \( \Rightarrow GJ = GC.\) Tương tự ta có GI = GB.
Vậy tứ giác BJIC là hình bình hành (hai đường chéo cắt nhau tại trung điểm mỗi đường).
- Đề kiểm tra 15 phút - Đề số 1 - Bài 1 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 2 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 3 - Bài 1 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 4 - Bài 1 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 5 - Bài 1 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 1 - Bài 2 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 2 - Bài 2 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 3 - Bài 2 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 4 - Bài 2 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 5 - Bài 2 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 1 - Bài 3 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 2 - Bài 3 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 3 - Bài 3 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 4 - Bài 3 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 5 - Bài 3 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 1 - Bài 4,5 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 2 - Bài 4,5 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 3 - Bài 4,5 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 4 - Bài 4,5 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 5 - Bài 4,5 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 6 - Bài 4, 5 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 7 - Bài 4,5 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 8 - Bài 4, 5 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 9 - Bài 4, 5 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 10 - Bài 4, 5 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 11 - Bài 4, 5 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 12 - Bài 4, 5 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 13 - Bài 4, 5 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 14 - Bài 4, 5 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 15 - Bài 4, 5 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 16 - Bài 4, 5 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 1 - Bài 6 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 3 - Bài 6 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 4 - Bài 6 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 1 - Bài 7 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 2 - Bài 7 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 3 - Bài 7 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 4 - Bài 7 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 5 - Bài 7 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 6 - Bài 7 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 7 - Bài 7 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 8 - Bài 7 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 9 - Bài 7 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 10 - Bài 7 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 1 - Bài 8 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 2 - Bài 8 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 3 - Bài 8 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 4 - Bài 8 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 5 - Bài 8 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 1 - Bài 9, 10 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 2 - Bài 9, 10 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 3 - Bài 9, 10 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 4 - Bài 9, 10 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 5 - Bài 9, 10 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 6 - Bài 9, 10 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 7 - Bài 9, 10 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 8 - Bài 9, 10 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 9 - Bài 9, 10 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 10 - Bài 9, 10 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 1 - Bài 11 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 2 - Bài 11 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 3 - Bài 11 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 4 - Bài 11 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 5 - Bài 11 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 6 - Bài 11 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 7 - Bài 11 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 1 - Bài 12 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 2 - Bài 12 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 3 - Bài 12 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 4 - Bài 12 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 5 - Bài 12 - Chương 1 - Hình học 8
- Bài 1. Tứ giác
- Bài 2. Hình thang
- Bài 3. Hình thang cân
- Bài 4. Đường trung bình của tam giác, của hình thang
- Bài 5. Dựng hình bằng thước và compa. Dựng hình thang
- Bài 6. Đối xứng trục
- Bài 7. Hình bình hành
- Bài 8. Đối xứng tâm
- Bài 9. Hình chữ nhật
- Bài 10. Đường thẳng song song với một đường thẳng cho trước
- Bài 11. Hình thoi
- Bài 12. Hình vuông
- Ôn tập chương I: Tứ giác
- Đề kiểm tra 15 phút - Chương 1 - Hình học 8
- Đề kiểm tra 45 phút ( 1 tiết) - Chương 1 - Hình học 8
