Đề kiểm tra 15 phút - Đề số 15 - Bài 4, 5 - Chương 1 - Hình học 8

Dựng hình thang cân ABCD \(\left( {AB// CD} \right)\) biết AB = a, đường chéo AC = m, góc giữa hai đường chéo là \(\alpha .\)

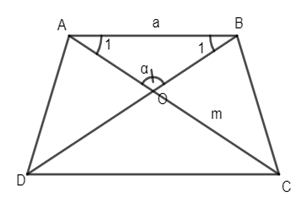
Giả sử hình thang cân ABCD đã dựng ta thấy tam giác cân AOB dựng được ngay biết \(AB = a,\widehat {AOB} = \alpha \)

\( \Rightarrow \widehat {{A_1}} = \widehat {{B_1}} = \dfrac{{{{180}^ \circ } - \alpha } }{2} = {90^ \circ } -\dfrac{\alpha  }{2}\)

Cần xác định hai đỉnh C và D.

+D thuộc BO sao cho BD = m.

+C thuộc tia AO sao cho AC = m.

Từ đó dựng \(\Delta AOB\) biết AB = a, \(\widehat {OAB} = \widehat {OBA} = {90^ \circ } - \dfrac{\alpha }{2}.\)

- Lấy D thuộc tia BO sao cho BD = m.

- Lấy C thuộc tia AO sao cho AC = m.

Ta được hình thang ABCD cần dựng.

Khi \(0 < \alpha  < {180^ \circ }\) bài toán luôn có nghiệm hình.