Đề kiểm tra 15 phút - Đề số 3 - Bài 9, 10 - Chương 1 - Hình học 8

Cho tam giác ABC có ba góc nhọn (AB < AC). Gọi AH là đường cao và M, N, P lần lượt là trung điểm cỉa AB, AC và BC. Gọi D là điểm đối xứng của H qua M.

a) Chứng minh tứ giác DAHB là hình chữ nhật.

b) Tìm điều kiện của \(\Delta ABC\(để AMPN là hình chữ nhật

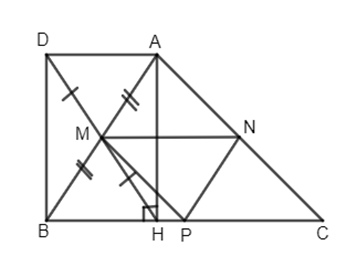
a) Ta có MA = MB (gt)

MD = MH (tính chất đối xứng)

\( \Rightarrow DAHB\) là hình bình hành.

Lại có \(\widehat {AHB} = {90^ \circ }\left( {gt} \right)\)

Do đó tứ giác DAHB là hình chữ nhật.

b) Ta có NP là đường trung bình của \(\Delta ABC\) (M, P là trung điểm của AC và BC) 

\(\Rightarrow NP// AB\) và \(NB = \dfrac{1 }{2}AB\) hay \(NP//AM\) và MP = AM.

Do đó AMPN là hình bình hành.

Hình bình hành AMPN là hình chữ nhật \( \Leftrightarrow \widehat {BAC} = {90^ \circ }\) .

Do đó \(\Delta ABC\) vuông tại A.