Đề kiểm tra 15 phút - Đề số 3 - Bài 12 - Chương 1 - Hình học 8

Cho hình vuông ABCD, trên tia đối của CB lấy điểm E, trên tia đối của DC lấy điểm F sao cho DF = BE. Qua E kẻ \(Ex// AF\) , qua F kẻ \(Fy// AE.\) Gọi P là giao điểm của Ex và Fy. Chứng minh rằng AEPF là hình vuông.

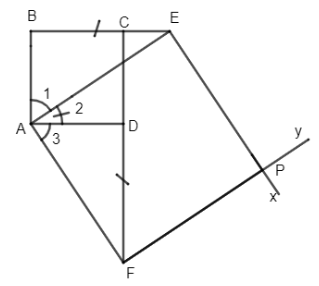
Xét hai tam giác ABE và ADF có:

AB = AD (gt)

BE = DF (giả thiết)

\( \Rightarrow \Delta ABE = \Delta ADF\left( {c.g.c} \right)\)

\( \Rightarrow \widehat {{A_1}} = \widehat {{A_3}}\) và AE = AF       (1)

Lại có \(\widehat {{A_1}} + \widehat {{A_2}} = 90^o \Rightarrow \widehat {{A_3}} + \widehat {{A_2}} = 90^o\) (2)

Mặt khác do \(EP// AF;EP// AE \Rightarrow AEPF\) là hình bình hành (3)

Từ (1),  (2) và (3) \( \Rightarrow AEPF\) là hình vuông