Đề kiểm tra 15 phút - Đề số 4 - Bài 1 - Chương 1 - Hình học 8

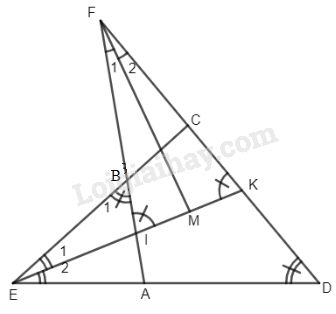
Tứ giác ABCD có các góc đối bù nhau. Các cạnh AD và BC cắt nhau tại E ; AB và DC cắt nhau tại F. Phân giác của hai góc CED và AFD cắt nhau tại M. Chứng minh rằng \(FM \bot EM.\)

Gọi I, K lần lượt là giao điểm của EM với AB và DC.

Ta có : \(\widehat {FIK} = \widehat {{E_1}} + \widehat {{D_1}}\) (góc ngoài của \(\Delta EIB\)) 

            \(\widehat {FKI} = \widehat {{E_2}} + \widehat D\)(góc ngoài của \(\Delta EKD\) )

Mà \(\widehat {{E_1}} = \widehat {{E_2}}\) (giả thiết)

\(\widehat {{B_1}} = \widehat D\) (cùng bù với \(\widehat {ABC}\) )

\( \Rightarrow \widehat {FIK}\) cân tại F.

Trong tam giác cân FIK có FM là phân giác nên FM cũng là đường cao.

Suy ra \(FM \bot IK\) hay \(FM \bot EM.\)