Đề kiểm tra 15 phút - Đề số 5 - Bài 11 - Chương 1 - Hình học 8

Cho tam giác ABC có ba góc nhọn, các đường cao AD và BE. Tia phân giác của góc DAC cắt BE, BC theo thứ tự tại I và K. Tia phân giác của góc EBC cắt AD, AC theo thứ tự tại M và N. Chứng minh tứ giác MINK là hình thoi.

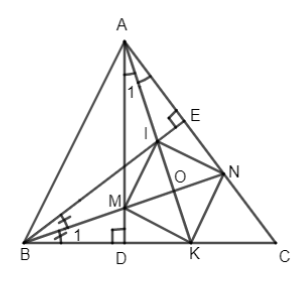
Ta có \(\widehat {EBC} = \widehat {DAC}\) (cùng phụ với \(\widehat C\) )

\(\widehat {AMN} = \widehat {BMD}\)(đối đỉnh) \( \Rightarrow \widehat {{A_1}} = \widehat {{B_1}}\)

Gọi O là giao điểm của AK và BN ta có:

\(\widehat {OAB} + \widehat {ABO} = \widehat {{A_1}} + \widehat {BAD} + \widehat {ABO}\)

                     \( = \widehat {{A_1}} + \widehat {BAD} + \left( {\widehat {ABD} - \widehat {{B_1}}} \right)\)

                     \( = \widehat {{A_1}} + \widehat {BAD} + \widehat {ABD} - \widehat {{B_1}} \)

                     \(= \widehat {BAD} + \widehat {ABD}\) (Vì \(\widehat {{A_1}} = \widehat {{B_1}}\) cmt)

                     \( = {90^ \circ }\) (vì \(\widehat {ADB} = {90^ \circ }\) )

Xét \(\Delta AOB\)

\(\Rightarrow \widehat {AOB} = {180^ \circ } - \left( {\widehat {OAB} + \widehat {ABO}} \right)\)\(\; = {180^ \circ } - {90^ \circ } = {90^ \circ }\)

Chứng tỏ \(AK \bot BM\) hay \(IK \bot MN\)  (1)

 \(\Delta MAN\) có AO là đường cao (cmt) đồng thời là phân giác (gt) \( \Rightarrow OM = ON.\) Tương tự với \(\Delta BIK\) ta có OI = OK. Vậy tứ giác MINK là hình bình hành, kết hợp với (1) ta có MINK là hình thoi.