Đề kiểm tra 15 phút - Đề số 3 - Bài 7 - Chương 1 - Hình học 8
a) I là trung điểm MP.
b) MNPQ là hình bình hành.
Lời giải
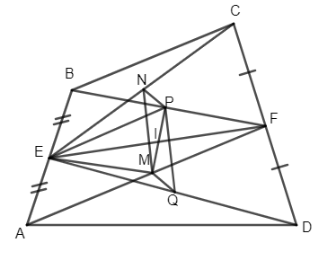
a) Ta có EP là đường trung bình của \(\Delta ABF\)
\( \Rightarrow EP// AF\) và \(EP = \dfrac{1}{ 2}AF.\)
M là trung điểm của AF (gt)
\( \Rightarrow MF = \dfrac{1}{ 2}AF\)
Do đó \(EP//MF\) và EP = MF. Vậy EPFM là hình bình hành.
I là giao điểm của MP và EF nên I là trung điểm của MP (1)
b) Tương tự ta chứng minh được \(EM//PF\) và \(EM = PF\) nên EPFM là hình bình hành \( \Rightarrow I\) là trung điểm của EF (vì I là trung điểm của MP)
Chứng minh tương tự ta có ENFQ là hình bình hành mà I là trung điểm EF \( \Rightarrow I\) là trung điểm của NQ
Từ (1) và (2) \( \Rightarrow MNPQ\) là hình bình hành (hai đường chéo cắt nhau tại trung điểm mỗi đường thẳng).
- Đề kiểm tra 15 phút - Đề số 1 - Bài 1 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 2 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 3 - Bài 1 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 4 - Bài 1 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 5 - Bài 1 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 1 - Bài 2 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 2 - Bài 2 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 3 - Bài 2 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 4 - Bài 2 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 5 - Bài 2 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 1 - Bài 3 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 2 - Bài 3 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 3 - Bài 3 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 4 - Bài 3 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 5 - Bài 3 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 1 - Bài 4,5 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 2 - Bài 4,5 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 3 - Bài 4,5 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 4 - Bài 4,5 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 5 - Bài 4,5 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 6 - Bài 4, 5 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 7 - Bài 4,5 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 8 - Bài 4, 5 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 9 - Bài 4, 5 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 10 - Bài 4, 5 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 11 - Bài 4, 5 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 12 - Bài 4, 5 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 13 - Bài 4, 5 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 14 - Bài 4, 5 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 15 - Bài 4, 5 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 16 - Bài 4, 5 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 1 - Bài 6 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 3 - Bài 6 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 4 - Bài 6 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 1 - Bài 7 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 2 - Bài 7 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 3 - Bài 7 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 4 - Bài 7 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 5 - Bài 7 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 6 - Bài 7 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 7 - Bài 7 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 8 - Bài 7 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 9 - Bài 7 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 10 - Bài 7 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 1 - Bài 8 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 2 - Bài 8 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 3 - Bài 8 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 4 - Bài 8 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 5 - Bài 8 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 1 - Bài 9, 10 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 2 - Bài 9, 10 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 3 - Bài 9, 10 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 4 - Bài 9, 10 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 5 - Bài 9, 10 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 6 - Bài 9, 10 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 7 - Bài 9, 10 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 8 - Bài 9, 10 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 9 - Bài 9, 10 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 10 - Bài 9, 10 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 1 - Bài 11 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 2 - Bài 11 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 3 - Bài 11 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 4 - Bài 11 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 5 - Bài 11 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 6 - Bài 11 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 7 - Bài 11 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 1 - Bài 12 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 2 - Bài 12 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 3 - Bài 12 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 4 - Bài 12 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 5 - Bài 12 - Chương 1 - Hình học 8
- Bài 1. Tứ giác
- Bài 2. Hình thang
- Bài 3. Hình thang cân
- Bài 4. Đường trung bình của tam giác, của hình thang
- Bài 5. Dựng hình bằng thước và compa. Dựng hình thang
- Bài 6. Đối xứng trục
- Bài 7. Hình bình hành
- Bài 8. Đối xứng tâm
- Bài 9. Hình chữ nhật
- Bài 10. Đường thẳng song song với một đường thẳng cho trước
- Bài 11. Hình thoi
- Bài 12. Hình vuông
- Ôn tập chương I: Tứ giác
- Đề kiểm tra 15 phút - Chương 1 - Hình học 8
- Đề kiểm tra 45 phút ( 1 tiết) - Chương 1 - Hình học 8
