Đề kiểm tra 15 phút - Đề số 6 - Bài 9, 10 - Chương 1 - Hình học 8

Cho hình bình hành ABCD. Phân giác các góc A, B, C, D cắt nhau tại các điểm M, N, P, Q. Chứng minh rằng tứ giác MNPQ là hình chữ nhật.

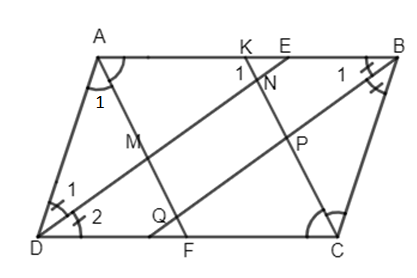
Gọi E là giao điểm của tia phân giác góc D và cạnh AB.

Ta có \(\widehat {{E_1}} = \widehat {{D_2}}\) (so le trong) mà \(\widehat D = \widehat B \Rightarrow \widehat {{D_2}} = \widehat {{B_1}}.\)

Do đó \(\widehat {{E_1}} = \widehat {{B_1}} \Rightarrow DE// BP.\)

Tương tự ta chứng minh được \({\rm{AF}}// CK.\) Vậy MNPQ là hình bình hành (1)

Mặt khác \(AB//CD \Rightarrow \widehat A + \widehat D = {180^ \circ }\)

\( \Rightarrow \dfrac{{\widehat A}}{2} + \dfrac{{\widehat D} }{ 2} = {90^ \circ }\) hay \(\widehat {{D_1}} + \widehat {{A_1}} = {90^ \circ }\)

Xét \(\Delta AMD \Rightarrow \widehat {AMD} = {90^ \circ } \)

\(\Rightarrow \widehat {NMQ} = {90^ \circ }\)     (2)

Từ (1) và (2) \( \Rightarrow MNPQ\) là hình chữ nhật.